DeepLearning-1 ConvolutionNetwork
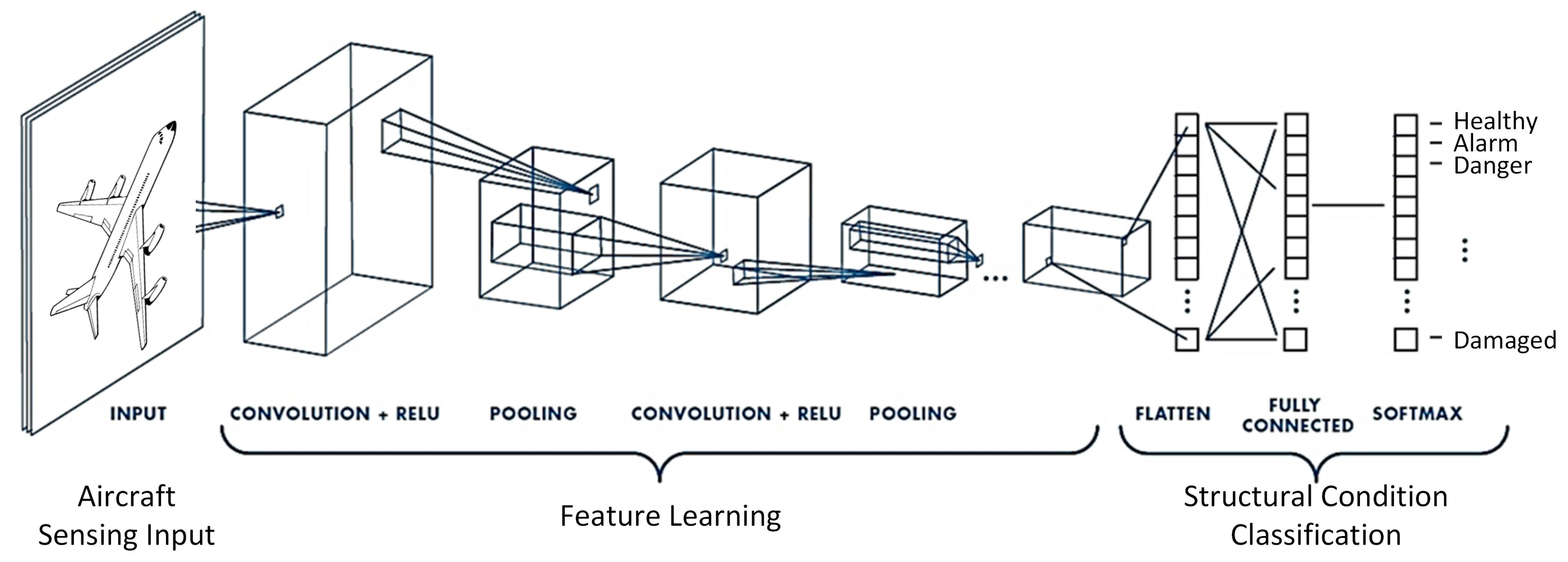
Introduction
Convolution neural network has been applied to different domains widely for feature extractor / filter. One of the most successful area is computer vision, in which convolution network is trained and used to extract the general feature we are interested in.
This article summarizes how forward passing and backpropagation works in CNN to train the CNN filters. Then some properties of CNN are mentioned.
Terms in CNN
N: number of data points/ samples in dataset
C: number of channel in one sample. Example: in RGB image, it has 3 channels: Red, Green, Blue
H: height of one data point matrix / amount of rows in one sample
W: width / amount of columns in one sample
x: input with shape (N, C, H, W)
y: output of convolution network
kernel/filter/weight: filter with trainable weights and shape of (KH, KW), where KH: height / rows of kernel, KW: width/ columns of kernel
b: bias term. One kernel correponds to one bias
stride: The number of pixel between adjacent receptive fields in horizonal, vertical directions.
padding: the number of rows, columns added to the boundaries/edges of a sample matrix.
Usually, we set the padding row/column values to zeros. We usually set padding = (1,1) or (2,2) to add 1 or 2 row(s)/column(s) to each edge of sample matrix
- Ho: height/ amount of rows of output fromm convolution
- Wo: width/ amount of columns of output from convolution
- Output shape from convolution network:
- Ho = 1 + (H + 2*padding - KH )/stride
- Wo = 1 + (W + 2*padding - KW )/stride
- if Ho, Wo are not integer, that means when moving the kernel along input, index out of range occurs. In this case, we can simply drop the last column/row that make index out of range. Or, we can add zero columns/rows to fill the out of range pieces in matrix.
How does CNN work
Forward pass in CNN
- Convolution with 1-D Input: without padding, stride =1, channel =1
After we define some terms above, let consider there is 1-D input X with shape: C=1, H=1, W=4 and 1-D kernel K with shape KH=1, KW = 3.
$$
X = [x1, x2, x3, x4], K = [w1, w2,w3]
$$
Then the output of convolution is
$$
Y = \begin{bmatrix}
y_1 \\
y_2
\end{bmatrix}
$$
where $y_1 = w_1 * x_1 + w_2 * x_2 + w_3 * x_3 +b$ and $y_2 = w_1 * x_2 + w_2 * x_3 + w_3 * x_4 +b$
where b is the bias term in convolution
- Convolution with 2-D Input: stride =1, no padding, channel =1
$$X = \begin{bmatrix}
x1 & x2 & x3 \\
x4 & x5 & x6 \\
x7 & x8 & x9
\end{bmatrix} ,
K = \begin{bmatrix}
w1 & w2 \\
w3 & w4
\end{bmatrix}
$$
Based on these equations,
- Ho = 1 + (H + 2*padding - KH )/stride
- Wo = 1 + (W + 2*padding - KW )/stride
we know that the output Y has shape H =2, W= 2:
$$
Y = \begin{bmatrix}
y1 & y2 \\
y3 & y4
\end{bmatrix}
$$
$$
y1 = sum( \begin{bmatrix}
x1 & x2 \\
x4 & x5
\end{bmatrix} * \begin{bmatrix}
w1 & w2 \\
w3 & w4
\end{bmatrix} ) +b = w1x1 + w2x2 + w3x4 + w4x5 + b
$$
where * is element-wise multiplication
Similarly, we have
$$
\begin{matrix}
y2 = w1x2 + w2x3 + w3x5 + w4x6 + b, \\
y3 = w1x4 + w2x5 + w3x7 + w4x8 + b, \\
y4 = w1x5 + w2x6 + w3x8 + w4x9 + b \\
\end{matrix}
$$
- Convolution with 2-D Input: with padding = (1,1) stride =1, channel =1
Here I add 1 row, 1 column zeros pad to four edges of 2-D matrix. Then the sample X becomes 4 by 4 matrix. After padding, we will do the same forward pass process as step 2.
$$
X = \begin{bmatrix}
0 & 0 & 0 & 0 & 0 \\
0 & x1 & x2 & x3 & 0 \\
0 & x4 & x5 & x6 & 0 \\
0 & x7 & x8 & x9 & 0 \\
0 & 0 & 0 & 0 & 0
\end{bmatrix}
$$
and
$$
K = \begin{bmatrix}
w1 & w2 & w3 \\
w4 & w5 & w6 \\
w7 & w8 & w9 \\
\end{bmatrix}
$$
The output Y becomes:
$$
Y = \begin{bmatrix}
y1 & y2 & y3 \\
y4 & y5 & y6 \\
y7 & y8 & y9 \\
\end{bmatrix}
$$
where
$$
y1 = w_1 * 0 + w_2 * 0 + w_3 * 0 + w_4 * 0 + w_5 * x_1 + w_6 * x_2 + w_7 * 0 +w_8 * x_4 + w_9 * x_5
$$
Let denote the $i^{th}$ row and $j^{th}$ column entry in output Y as $y_{i,j}$, the $h^{th}$ row and $w^{th}$ column entry in kernel K as $w_{h,w}$, the number of stride as $s$.
We can write down the formula to compute every entry in output Y:
$$
y_{i,j} = \sum_{h=1}^{KH}\sum_{w = 1}^{KW} w_{h,w} * x_{s * i+h-1, s * j+w -1}
$$
- Convolution with 2-D Input: with channel =3, padding = (1,1) stride =1
when channel of sample X is more than 1, we will need the amount of kernels K equal to the number of input channel $C_{in}$.
Example: Input X with Channel C=3
$$
X_R = \begin{bmatrix}
xr1 & xr2 & xr3 \\
xr4 & xr5 & xr6 \\
xr7 & xr8 & xr9
\end{bmatrix}
$$
$$
X_G = \begin{bmatrix}
xg1 & xg2 & xg3 \\
xg4 & xg5 & xg6 \\
xg7 & xg8 & xg9
\end{bmatrix}
$$
$$
X_B = \begin{bmatrix}
xb1 & xb2 & xb3 \\
xb4 & xb5 & xb6 \\
xb7 & xb8 & xb9
\end{bmatrix}
$$
Then we will need one kernel for each input channel. Hence we will have 3 kernels $K_R, K_G,K_B$. The output of this convolution network is the sum of all convolution output
$$
Y = conv(X_R, K_R) + conv(X_G, K_G) + conv(X_B, K_B)
$$
In this cases, the output channel is still C= 1. If we want the output channel to be more than 1. Let say the output channel $C_{out}$ =3, then we have $C_{out} * C_{in}$ kernels in total and each kernel has shape of $W_o * H_o$.
Hence we will have parameters with amount of $C_{out} * C_{in} * W_o * H_o$ or $C_{out} * C_{in} * (1 + (H + 2 * pad - KH) / stride ) * (1 + (W + 2 * pad - KW) / stride )$
Chain Rule
Before talking about how to update the weight in kernel, let talk about the chain rule first.
Denote loss function as $L(y_p, y_t)$, where $y_p$ is prediction / output from estimator and $y_p =f_w(x)$ is a function of input x, $y_t$ is target, where x, y,w are all scalar values
Let: $y_p = f_w(x) =wx$
$$
L(w) = L(y_p, y_{t}) = (y_p - y_{t})^2 = (f_w(x) - y_{t})^2 = (wx - y_{t})^2
$$
Then in chain rule to find the gradient of weight w, we have
$$
\nabla_w L(w) = \frac{dL(w)}{dw} = \frac{dL}{dy_p} * \frac{dy_p}{dw} = [2 *(y_p - y_t)] * [x] = 2x(wx - y_t)
$$
By chain rule, we can extend $ \frac{dL}{dy_p} * \frac{dy_p}{dw}$ to $\frac{dL}{dy_p} * \frac{dy_p}{dy_1} * \frac{dy_1}{dy_2} *…\frac{dy_i}{dw}$ in many terms
Backpropagation in CNN
Let’s go back the feed forward step in CNN, we have equation
$$
y_{i,j} =f_w(x) = \sum_{h=1}^{KH}\sum_{w = 1}^{KW} w_{h,w} * x_{s * i+h-1, s * j+w -1}
$$
Where the output vector of convolution is $Y$ and $y_{i,j}$ is the $i^{th}$ row and $j^{th}$ column entry of Y. $Y^t$ is the target. $x_{i,j}$ is the $i^{th}$ row and $j^{th}$ column entry of input X. Define loss function $L(w)$ .
Then gradient of weight $w_{h,w}$ in kernel is obtained by
$$
\frac{dL(w)}{dw_{h,w}} = \sum_{i=1}^{H}\sum_{j=1}^{W}\frac{dL}{dy_{i,j}} * \frac{dy_{i,j}}{dw_{h,w}}
$$
Example:
$$
X = \begin{bmatrix}
x_{11} & x_{12} & x_{13} \\
x_{21} & x_{22} & x_{23} \\
x_{31} & x_{32} & x_{33}
\end{bmatrix} , K = \begin{bmatrix}
w_{11} & w_{12} \\
w_{21} & w_{22}
\end{bmatrix}
$$
$$
Y = \begin{bmatrix}
y_{11} & y_{12} \\
y_{21} & y_{22}
\end{bmatrix}
$$
Let Loss function be $L(w) = 0.5* \sum_i\sum_j (y_{i,j} - y^{t}_{i,j})^2$
and we have
$$
\frac{dL}{dy_{i,j}} = (y_{i,j} - y^{t}_{i,j})
$$
$$
\frac{dL}{dy} = \begin{bmatrix}
\frac{dL}{dy_{11}} & \frac{dL}{dy_{12}} \\
\frac{dL}{dy_{21}} & \frac{dL}{dy_{22}}
\end{bmatrix}
$$
$$
\frac{dy_{11}}{dw_{11}} = \frac{d(w_{11} * x_{11} + w_{12} * x_{12} + w_{21} * x_{21} + w_{22} * x_{22} +b)}{dw_{11}}
$$
$$
\frac{dy_{11}}{dw_{11}} = x_{11}
$$
Similarly, we have
$$
\frac{dy}{dw_{11}} = \begin{bmatrix}
\frac{dy_{11}}{dw_{11}} & \frac{ddy_{12}}{dw_{11}} \\
\frac{ddy_{21}}{dw_{11}} & \frac{ddy_{22}}{dw_{11}}
\end{bmatrix} = \begin{bmatrix}
x_{11} & x_{12} \\
x_{21} & x_{22}
\end{bmatrix}
$$
Finally, gradient of weight $w_{11}$ becomes
$$
\frac{dL}{dw_{11}} = sum(\frac{dL}{dy} * \frac{dy}{dw_{11}} ) = \sum_{i=1}^{2}\sum_{j=1}^{2}\frac{dL}{dy_{i,j}} * \frac{dy_{i,j}}{dw_{1,1}}
$$
$$
\frac{dL}{dw_{11}} = \sum_{i=1}^{2}\sum_{j=1}^{2} (y_{i,j}-y^t_{i,j})*x_{i,j}
$$
where * is element-wise multiplication Repeat doing this, we can find the gradient for all weights in all kernels.
Properties in CNN
- the weight matrix in CNN is small and save memory compared with traditional dense network.
For example, if we have an 1818 input matrix we want to output a 3x3 matrix, we can either use a 16x16 convolution kernel with stride =1, or 9 3x3 kernels to do this.
In this case, 933 is smaller than 1616. Hence CNN with deeper convolution network and small filter can save memory - Updating weights in CNN is fast, as the weight / kernel is small
- CNN can be used for transfer learning by transferring learned kernels
- CNN can be used for down-sampling data, reducing data size.
For example, in ResNet, it uses pixel convolution: kernel size =1 * 1 and stride =2 to down sample data by half of original size in each channel of matrix
Reference
[1] https://towardsdatascience.com/backpropagation-in-a-convolutional-layer-24c8d64d8509