Recommendation-System-3-DeepFM

Background

在推荐系统里面学习低阶和高阶的feature，将feature 进行交叉组合挖掘数据的信息一直需要花费大量的时间精力进行feature engineering。组合特征大牛们研究过组合二阶特征，三阶甚至更高阶，但是面临一个问题就是随着阶数的提升，复杂度就成几何倍的升高。这样即使模型的表现更好了，但是推荐系统在实时性的要求也不能满足了。所以很多模型的出现都是为了解决另外一个更加深入的问题：如何更高效的学习特征组合？

为了进行通过特征交叉更加高效学习高阶和低阶的特征，大牛们曾经对研究过FM(factorization machine), FFM (field-aware factorization machine) 对特征进行交叉和研究更加高阶的特征
(注意FM的特征交叉相对于直接在logistics regression对特征进行相乘交叉而已，通过用embedding的思想先把sparse feature $x_j$ 进行embedding转换成dense的vector 然后再对不同的特征交叉， 这样的好处在避免了$x_ix_j$特征交叉时只要有一个特征是0就会变成0这样更加容易稀疏的缺陷).
然而FM， FFM的方法把特征进行交叉的问题在于随着交叉的order越高，计算复杂度越大。

另外一种方法是利用DNN对更加高阶的非线性特征进行学习。但是这种方法会导致model的参数因为sparse的feature维度太高而导致参数过多的难以训练的问题。

为了解决这几个问题，研究人员曾经把FM， DNN和embedding进行结合。先通过embedding把sparse feature进行降维学习到dense的vector同时也泛化了feature，之后再通过类似FM的feature intersection 特征交叉的形式(比如inner product和outer product)将feature 进行组合并得到高阶的feature，最后再用DNN进行特征学习，而这也引向了PNN的思想。下图为PNN的结构。

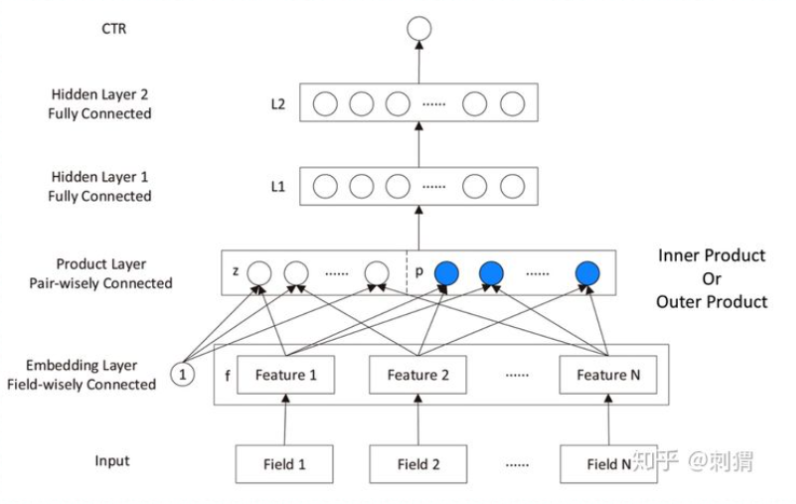
不过PNN的问题在于它通过串行的形式把feature变成高阶feature之后，低阶的feature不能很好表达(因为所有输入的feature都被投影转换后丢失了原来低阶特征的信息)。

为了解决这个问题，后来研究人员把Google的wide&deep的model的并行结构(wide model+ deep model)和 类似FM的feature crossing的方式进行结合，把高阶特征和低阶特征同时并行分开学习而这个也就是DeepFM的思想

Motivation

在DeepFM (deep factorization machine) 里面，它通过把Factorization Machine， Embedding，Wide&Deep model 的思想进行结合从而达到以下的效果：

• No Feature Engineering
  和wide&deep 相比， DeepFM 不用做feature engineering对feature进行组合，DeepFM可以直接通过FM方式把数据特征自动组合

• Learn low-order Feature Intersection and high-order Feature Intersection
  相对于PNN， DeepFM通过利用并行的方式对高阶和低阶特征进行组合，而不会影响低阶特征的表达和学习

• Share the same input and embedding vector
  对于不同的用户的数据输入，DeepFM用相同的embedding vectors进行转换，用户的sparse的数据相对于是对embedding的vector进行选择，这样可以有效降低模型的空间复杂度

How DeepFM work

模型的结构与原理

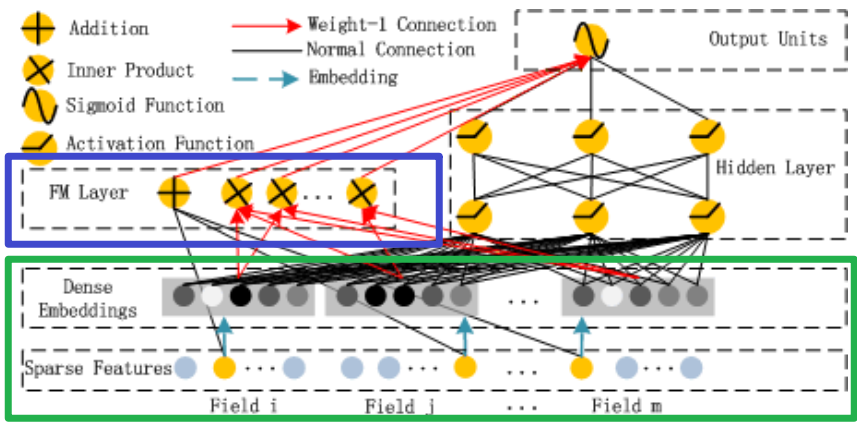
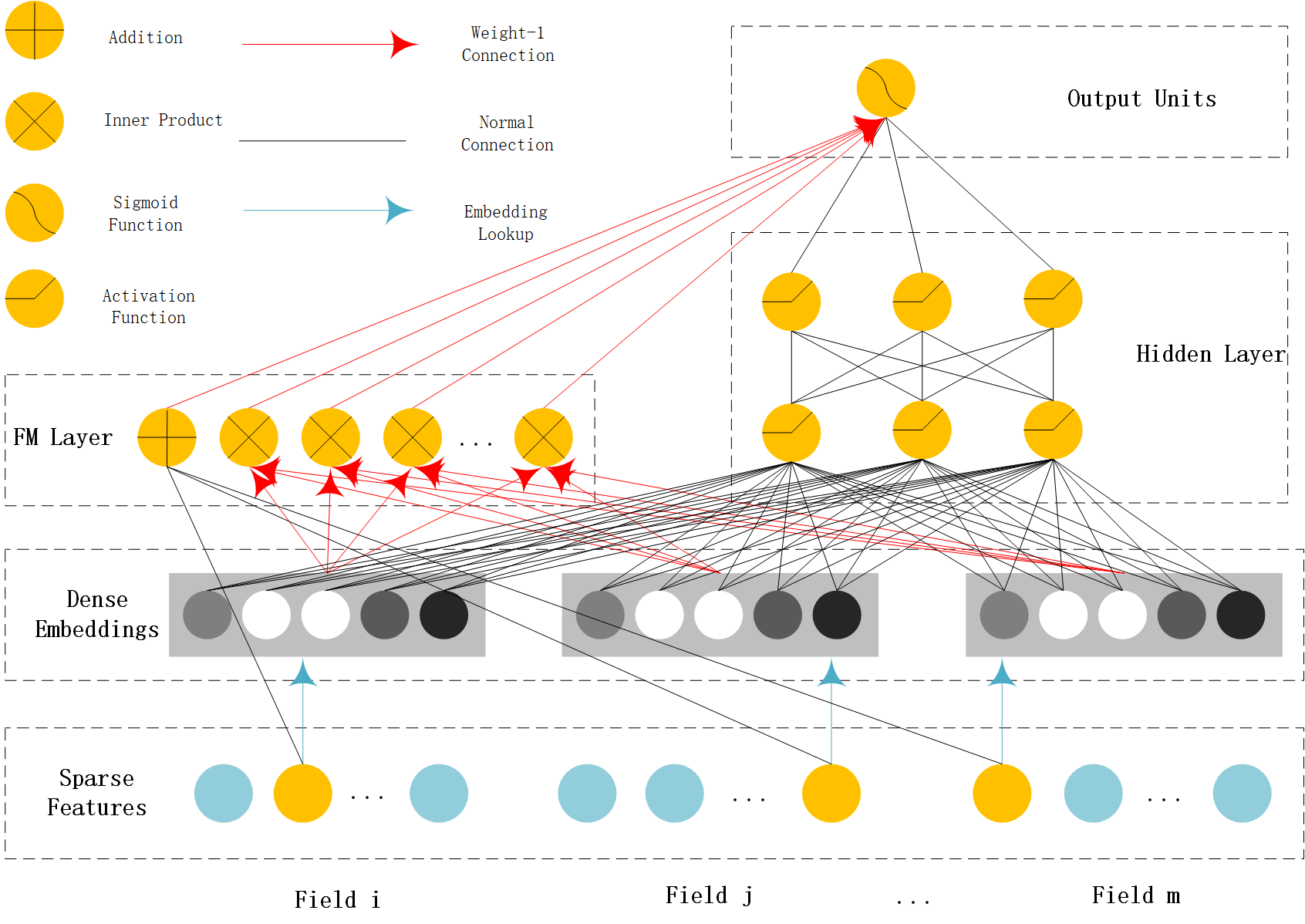
前面的Field和Embedding处理是和前面的方法是相同的，如上图中的绿色部分；DeepFM将Wide部分替换为了FM layer如上图中的蓝色部分

这幅图其实有很多的点需要注意，很多人都一眼略过了，这里我个人认为在DeepFM模型中有三点需要注意：

• Deep模型部分
• FM模型部分
• Sparse Feature中黄色和灰色节点代表什么意思

FM model

详细内容参考FM模型部分的内容，下图是FM的一个结构图，从图中大致可以看出FM Layer是由一阶特征和二阶特征Concatenate到一起在经过一个Sigmoid得到logits（结合FM的公式一起看），所以在实现的时候需要单独考虑linear部分和FM交叉特征部分。

$$
y_{FM}(x) = w_0+\sum_{i=1}^N w_ix_i + \sum_{i=1}^N \sum_{j=i+1}^N v_i^T v_j x_ix_j
$$

Deep model

Deep架构图

Deep Module是为了学习高阶的特征组合，在上图中使用用全连接的方式将Dense Embedding输入到Hidden Layer，这里面Dense Embeddings就是为了解决DNN中的参数爆炸问题，这也是推荐模型中常用的处理方法。

Embedding层的输出是将所有id类特征对应的embedding向量concat到到一起输入到DNN中。其中$v_i$表示第i个field的embedding，m是field的数量。
$$
z_1=[v_1, v_2, …, v_m]
$$
上一层的输出作为下一层的输入，我们得到：
$$
z_L=\sigma(W_{L-1} z_{L-1}+b_{L-1})
$$
其中$\sigma$表示激活函数，$z, W, b $分别表示该层的输入、权重和偏置。

最后进入DNN部分输出使用sigmod激活函数进行激活：
$$
y_{DNN}=\sigma(W^{L}a^L+b^L)
$$

Properties

优点

• 结合了Wide&Deep, FM的特点，在通过特征进行交叉(feature intersection)来得到更高阶的特征并同时学习高阶特征和低阶特征
• 不用进行特别精细的feature engineering （wide&Deep 在wide的模型里面还是需要人工特征组合，比较wide model里面feature intersection不够）
• 通过embedding和field input的思想将sparse的特征进行降维同时可以share相同的embedding vector，降低模型的复杂度

Comparison of deep models for CTR prediction

model	No Feature Pre-training	High-order	Low-order	No Features Engineering
FNN	×	√	×	√
PNN	√	√	×	√
Wide & Deep	√	√	√	×
DeepFM	√	√	√	√

缺点

• 对于 FM部分的训练会相对较慢

FM的公式是一个通用的拟合方程，可以采用不同的损失函数用于解决regression、classification等问题，比如可以采用MSE（Mean Square Error）loss function来求解回归问题，也可以采用Hinge/Cross-Entropy loss来求解分类问题。当然，在进行二元分类时，FM的输出需要使用sigmoid函数进行变换，该原理与LR是一样的。直观上看，FM的复杂度是 $O(kn^2)$ 。但是FM的二次项可以化简，其复杂度可以优化到 $O(kn)$ 。由此可见，FM可以在线性时间对新样本作出预测。

证明推理见 link：

$\begin{array}{cc}
\sum_{i=1}^{n-1}{\sum_{j=i+1}^{n}{<v_i,v_j>x_ix_j}}\\
= \frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n <v_i,v_j>x_ix_j -\frac{1}{2}\sum_{i=1}^n <v_i,v_i>x_ix_i\\
= \frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\sum_{f=1}^k v_{if}v_{jf}x_ix_j - \frac{1}{2}\sum_{i=1}^n\sum_{f=1}^k v_{if}v_{if}x_ix_i\\
= \frac{1}{2}\sum_{f=1}^k [(\sum_{i=1}^nv_{if}x_i)(\sum_{j=1}^nv_{jf}x_j) - \sum_{i=1}^nv_{if}^2x_{i}^2]\\
\end{array}$
由于第一个sum的loop时间是O(k), 而计算$(\sum_{j=1}^nv_{jf}x_j)$只需要1次就可以得到中括号里面的term所以是O(n)最后相乘起来时间复杂度变成O(kn)

其中

• 没有考虑到用户的兴趣和过去浏览的历史的问题，只是单纯在对feature进行交叉，没有考虑用户在时间上的行为变化，也不能进行个性化推荐
• FM的部分可能需要FTRL优化器进行更新

Questions

Code

def DeepFM(linear_feature_columns, dnn_feature_columns):
    # 构建输入层，即所有特征对应的Input()层，这里使用字典的形式返回，方便后续构建模型
    dense_input_dict, sparse_input_dict = build_input_layers(linear_feature_columns + dnn_feature_columns)

    # 将linear部分的特征中sparse特征筛选出来，后面用来做1维的embedding
    linear_sparse_feature_columns = list(filter(lambda x: isinstance(x, SparseFeat), linear_feature_columns))

    # 构建模型的输入层，模型的输入层不能是字典的形式，应该将字典的形式转换成列表的形式
    # 注意：这里实际的输入与Input()层的对应，是通过模型输入时候的字典数据的key与对应name的Input层
    input_layers = list(dense_input_dict.values()) + list(sparse_input_dict.values())

    # linear_logits由两部分组成，分别是dense特征的logits和sparse特征的logits
    linear_logits = get_linear_logits(dense_input_dict, sparse_input_dict, linear_sparse_feature_columns)

    # 构建维度为k的embedding层，这里使用字典的形式返回，方便后面搭建模型
    # embedding层用户构建FM交叉部分和DNN的输入部分
    embedding_layers = build_embedding_layers(dnn_feature_columns, sparse_input_dict, is_linear=False)

    # 将输入到dnn中的所有sparse特征筛选出来
    dnn_sparse_feature_columns = list(filter(lambda x: isinstance(x, SparseFeat), dnn_feature_columns))

    fm_logits = get_fm_logits(sparse_input_dict, dnn_sparse_feature_columns, embedding_layers) # 只考虑二阶项

    # 将所有的Embedding都拼起来，一起输入到dnn中
    dnn_logits = get_dnn_logits(sparse_input_dict, dnn_sparse_feature_columns, embedding_layers)
    
    # 将linear,FM,dnn的logits相加作为最终的logits
    output_logits = Add()([linear_logits, fm_logits, dnn_logits])

    # 这里的激活函数使用sigmoid
    output_layers = Activation("sigmoid")(output_logits)

    model = Model(input_layers, output_layers)
    return model

Reference

[1] Datawhale: https://github.com/datawhalechina/team-learning-rs/blob/master/DeepRecommendationModel/DeepFM.md
[2] zhihu: https://zhuanlan.zhihu.com/p/50692817
[3] CSDN: https://blog.csdn.net/ISMedal/article/details/100578354
[4] https://blog.csdn.net/a819825294/article/details/51218296
[5] DeepFM Paper: https://arxiv.org/pdf/1703.04247.pdf