Recommendation-System-4-NFM

Background

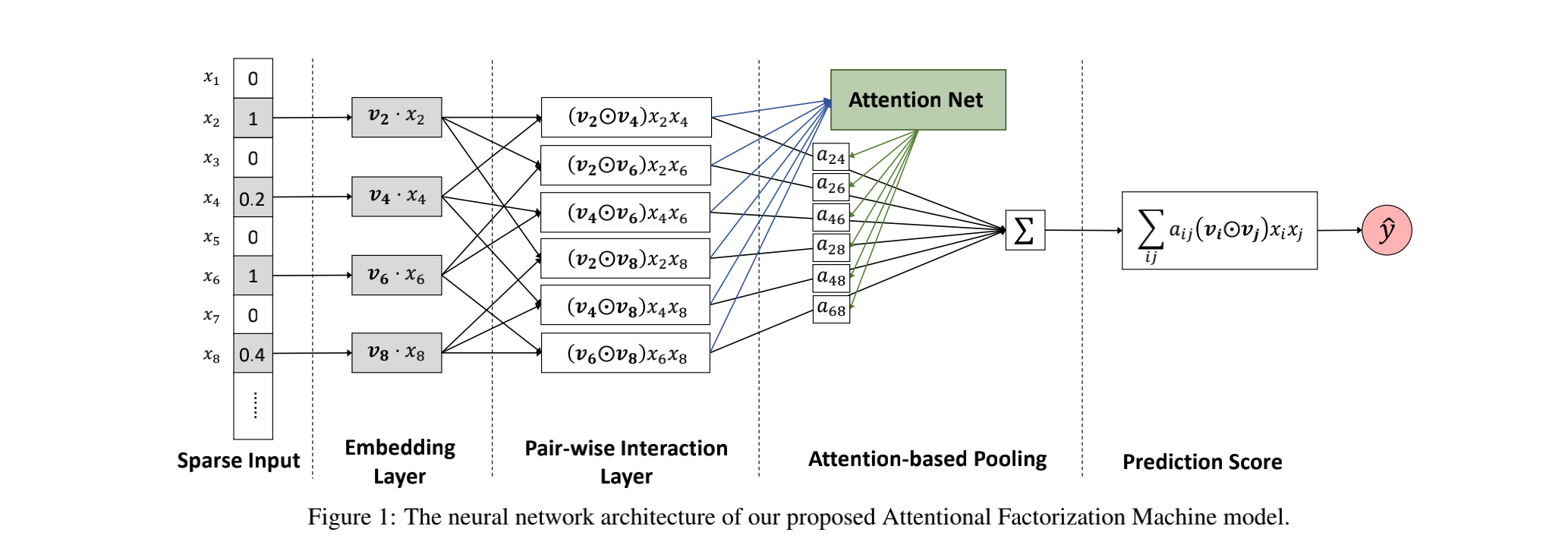
NeuralFM (Neural Factorization Machines)是2017年由新加坡国立大学的何向南教授等人在SIGIR会议上提出的一个模型，这个模型可以看成是直接把FM，Neural network 和embedding的简单粗暴的结合 （原来论文这么好发的吗？）

Motivation

这个模型考虑的问题是 FM 模型只考虑了一阶和二阶的特征，然而对更加高阶的特征没有学习到，这样无法对生活中更加复杂和有规律的数据进行挖掘和学习。FM的公式如下， 它只考虑到一阶和二阶的特征组合。第二个term是inner product。
$$
y_{N F M}(x)=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+ \sum_{i=1}^{n}\sum_{j=i+1}^{n} <v_iv_j , x_{i}x_{j}>
$$

为了解决这个局限性问题，何向南教授通过简单粗暴的方法直接把FM的二阶特征的组合的部分换成神经网络，并将sparse的feature在网络中先进行embedding降维再交叉结合从而得到学习更加高阶非线性特征的效果， 更新后的公式如下：

$$
y_{N F M}(x)=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+f(x)
$$

其中f(x) 是DNN的部分.

NeuralFM 原理

Neural FM 的模型结构如下：
橙色框框代表FM里面linear feature 的一阶特征组合，而对于sparse的特征先通过embedding生成dense vector然后把dense vector用于一阶的特征组合(橙色框框)以及bi-interactoin pooling layer 的高阶特征交叉进行高阶特征的学习（绿色框框）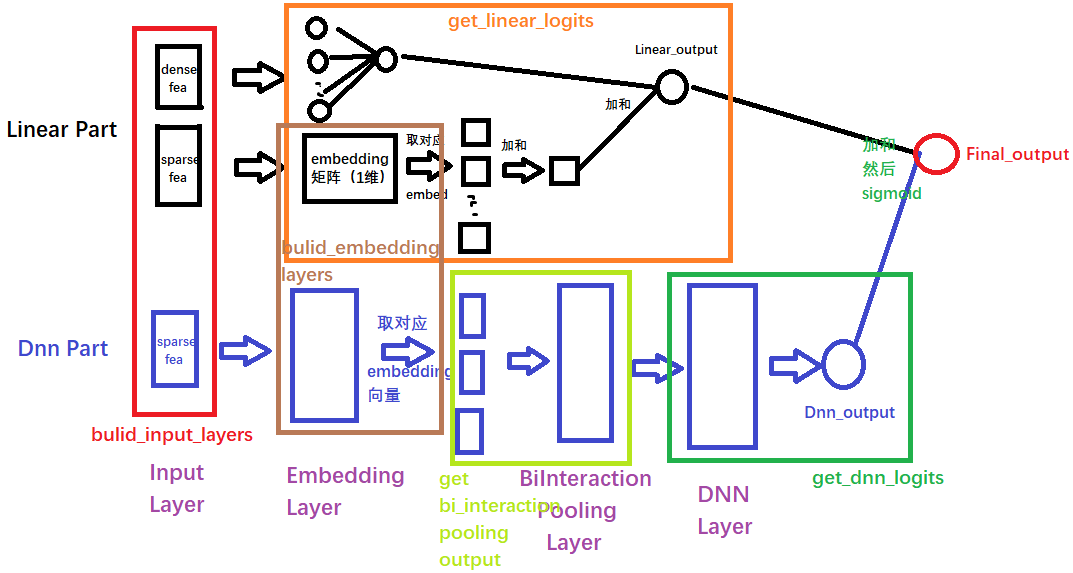

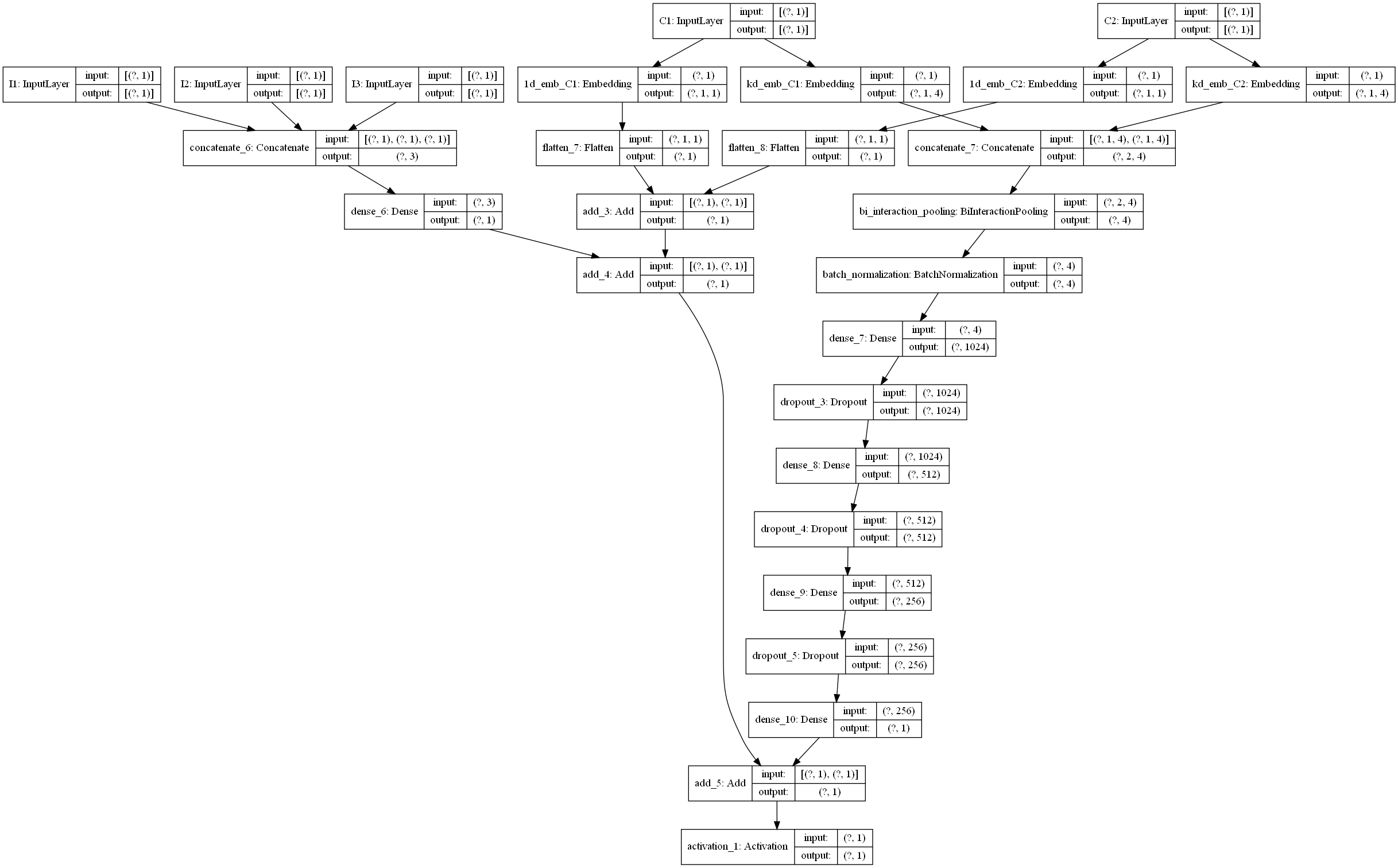
NeuralFM 的$f(x)$ 部分的结构如下：

NeuralFM的DNN部分由 Sparse input, Embedding layer, B-intersection Layer, Hidden layers (Deep model), prediction output组成

Input Layer

输入层的特征里面 每一个cell相当于一个 sparse feature， 每个feature一般是先one-hot, 然后会通过embedding，生成纬度低的dense vector，假设$v_i \in R^{k}$为第$i$个特征的embedding向量， 那么$V_{x}={x_{1} v_{1}, \ldots, x_{n} v_{n}}$表示的下一层的输入特征。这里带上了$x_i$是因为很多$x_i$转成了One-hot之后，出现很多为0的， 这里的$x_iv_i$ 是一个embedding的vector 而 $x_i$不等于0的那些特征向量，相当于$x_i$ 通过lookup table 方式选择 embedding vector $v_i$.

Bi-Interaction Pooling layer

在Embedding层和神经网络之间加入了特征交叉池化层是本网络的核心创新了，正是因为这个结构，实现了FM与DNN的无缝连接， 组成了一个大的网络，且能够正常的反向传播。假设$V_{x}$是所有特征embedding的集合， 那么在特征交叉池化层的操作：

$$
f_{B I}(V_{x})=\sum_{i=1}^{n} \sum_{j=i+1}^{n} x_{i} v_{i} \odot x_{j} v_{j}
$$

$\odot$表示两个向量的元素积操作(element-wise multiplication, 这个不清楚可以google一下)，即两个向量对应维度相乘得到的元素积向量（可不是点乘)

个人认为在 $x_{i} v_{i} \odot x_{j} v_{j}$ 里面它的结构是和$v_i,v_j$相同大小的特征dense vector。$f_{B I}(V_{x})$是多个dense vector的简单直接交叉element-wise相乘后相加的结果。这个方法其实也是挺直接
Bi-Interaction层不需要额外的模型学习参数，更重要的是它在一个线性的时间内完成计算，和FM一致的，即时间复杂度为$O(k N_{x})$，$N_x$为embedding向量的数量。参考FM，可以将上式转化为证明推理见 link：

$$
f_{B I}(V_{x})=\frac{1}{2}[(\sum_{i=1}^{n} x_{i} v_{i})^{2}-\sum_{i=1}^{n}(x_{i} v_{i})^{2}]
$$

Hidden Layer

这一层就是全连接的神经网络， DNN在进行特征的高层非线性交互上有着天然的学习优势，公式如下：

$$
\begin{array}{cc}
a_1 = \sigma(W_1f_{BI}(V_x) +b_1) \\
a_2 = \sigma(W_2a_1 +b_2) \\
… \\
a_{i+1} = \sigma(W_ia_i +b_i) \\
\end{array}
$$

这里的$\sigma_i$是第$i$层的激活函数，hidden layer里面一般是ReLu函数而不是logistics 来防止梯度消失问题， $f_{BI}(V_x)$是交叉后的embedding的dense vector。

Prediction Layer

这个就是最后一层的结果直接过一个隐藏层，但如果这里是回归问题，没有加sigmoid激活，如果是分类问题，需要加上logistic 或softmax的 activation function：

$$
f({x})={h}^{T} {z}_{L}
$$

在NeuralFM的DNN这一部分，为了减少DNN的很多负担，一般只需要很少的隐藏层就可以学习到高阶特征信息。当然可以像其他深度模型一样通过添加Dropout, Batch normalization, ResBlock 等方法进行进行更加深度的feature的学习已经抑制过拟合，梯度消失等问题。

Properties

优点

• NFM 通过简单粗暴直接的方式把FM的二阶特征组合部分换成DNN的方式学习到更加高阶非线性的特征，很容易理解
• 计算简单直接linear logit + embedding 的DNN的部分就完事了，而且由于DNN一般来说比较浅就能学习高阶的特征，训练也不难
• 能够学习低阶特征和高阶特征
• 能够通过embedding有效解决sparse feature带来的训练看你的问题，不用像wide&deep那样需要额外的FTRL的optimization的方法进行优化

缺点

• 和DeepFM相比，NeuralFM 有点像把DeepFM里面的FMmodel和Deep model 串起来的感觉。相对于DeepFM, NFM没有把低阶特征直接交叉，只是要么把低阶特征直接线性相加，要么把他们通过embedding进行投影到高阶general的特征再直接相加，所以感觉对低阶特征交叉组合方面不太好。

Code

def NFM(linear_feature_columns, dnn_feature_columns):
    """
    搭建NFM模型，上面已经把所有组块都写好了，这里拼起来就好
    :param linear_feature_columns: A list. 里面的每个元素是namedtuple(元组的一种扩展类型，同时支持序号和属性名访问组件)类型，表示的是linear数据的特征封装版
    :param dnn_feature_columns: A list. 里面的每个元素是namedtuple(元组的一种扩展类型，同时支持序号和属性名访问组件)类型，表示的是DNN数据的特征封装版
    """
    # 构建输入层，即所有特征对应的Input()层， 这里使用字典的形式返回， 方便后续构建模型
    # 构建模型的输入层，模型的输入层不能是字典的形式，应该将字典的形式转换成列表的形式
    # 注意：这里实际的输入与Input()层的对应，是通过模型输入时候的字典数据的key与对应name的Input层
    dense_input_dict, sparse_input_dict = build_input_layers(linear_feature_columns+dnn_feature_columns)
    input_layers = list(dense_input_dict.values()) + list(sparse_input_dict.values())
    
    # 线性部分的计算 w1x1 + w2x2 + ..wnxn + b部分，dense特征和sparse两部分的计算结果组成，具体看上面细节
    linear_logits = get_linear_logits(dense_input_dict, sparse_input_dict, linear_feature_columns)
    
    # DNN部分的计算
    # 首先，在这里构建DNN部分的embedding层，之所以写在这里，是为了灵活的迁移到其他网络上，这里用字典的形式返回
    # embedding层用于构建FM交叉部分以及DNN的输入部分
    embedding_layers = build_embedding_layers(dnn_feature_columns, sparse_input_dict, is_linear=False)
    
    # 过特征交叉池化层
    pooling_output = get_bi_interaction_pooling_output(sparse_input_dict, dnn_feature_columns, embedding_layers)
    
    # 加个BatchNormalization
    pooling_output = BatchNormalization()(pooling_output)
    
    # dnn部分的计算
    dnn_logits = get_dnn_logits(pooling_output)
    
    # 线性部分和dnn部分的结果相加，最后再过个sigmoid
    output_logits = Add()([linear_logits, dnn_logits])
    output_layers = Activation("sigmoid")(output_logits)
    
    model = Model(inputs=input_layers, outputs=output_layers)
    
    return model

Reference

[1] datawhale: https://github.com/datawhalechina/team-learning-rs/blob/master/DeepRecommendationModel/NFM.md

[2] FM https://www.jianshu.com/p/152ae633fb00

[3] 原paper https://arxiv.org/pdf/1708.05027.pdf