Deep Learning35 minutes read (About 5175 words)  0 visits

GNN-3-NodeEmbedding

Node Embedding and Node Prediction

1. Introduction

首先回顾一下上一篇文章关于MessagePassing的GNN的内容。在GNN的MessagePassing里面，每个node代表一个subject，然后edge代表subject之间的关系。而MessagePassing一句话总结就是让每个node的特征(node representation 或node embedding)通过对应的neighbor nodes的信息进行聚集并用于更新每个node
的信息，从而学习到更好的node embedding表达。之后我们可以对学习到的node embedding里面每个node的特征向量输入到classifier里面进行node classification识别subject的类别。除了node classification外，node embedding还能用来做edge classification， graph classification 等任务。

而这次项目的目的是要实现GNN图神经网络并进行实践应用到Cora (scientific publications)科学文献dataset里面，并对每篇文章进行分类和预测文章的类别。这次的项目的大概流程是:

  1. Introduction to Cora Dataset: 简单介绍一下Cora论文数据集的构成
  2. Data Visualization: 对Cora数据集的node representation 和class 进行可视化
  3. Modeling and training: 搭建和训练MLP, GCN, GAT等模型对node 进行classification以及测试
  4. Visualize learned node representation: 将学到的node representation进行可视化分析每个类分布的不同
  5. Assignment: 尝试其他不同的Dataset看一下不同GNN的效果
  6. Conclusion: 总结一下学到什么

2. Data Description

这里先来介绍Coras Dataset的内容，Coras Dataset 的解释可以从官网找到: https://linqs.soe.ucsc.edu/data
Coras dataset content:

  • Number of nodes: 2708 nodes. 每个node代表一篇论文
  • Number of edges/links: 5429条无向的边，如果用有向的边表示就是10556条
  • Number of class: 8. 总共有7个类别的论文
  • Dimension of node representation: 1433. 字典的大小为1433每个词用0,1 表示文章有没有那个词. 每篇文章的node representation就有1433
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from torch_geometric.datasets import Planetoid
from torch_geometric.transforms import NormalizeFeatures

dataset = Planetoid(root='./dataset', name='Cora', transform=NormalizeFeatures())

print()
print(f'Dataset: {dataset}:')
print('======================')
print(f'Number of graphs: {len(dataset)}')
print(f'Number of features: {dataset.num_features}')
print(f'Number of classes: {dataset.num_classes}')

data = dataset[0]  # Get the first graph object.

print()
print(data)
print('======================')

# Gather some statistics about the graph.
print(f'Number of nodes: {data.num_nodes}')
print(f'Number of edges: {data.num_edges}')
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}')
print(f'Number of training nodes: {data.train_mask.sum()}')
print(f'Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}')
print(f'Contains isolated nodes: {data.contains_isolated_nodes()}')
print(f'Contains self-loops: {data.contains_self_loops()}')
print(f'Is undirected: {data.is_undirected()}')
Dataset: Cora():
======================
Number of graphs: 1
Number of features: 1433
Number of classes: 7

Data(edge_index=[2, 10556], test_mask=[2708], train_mask=[2708], val_mask=[2708], x=[2708, 1433], y=[2708])
======================
Number of nodes: 2708
Number of edges: 10556
Average node degree: 3.90
Number of training nodes: 140
Training node label rate: 0.05
Contains isolated nodes: False
Contains self-loops: False
Is undirected: True

1
data.train_mask,data.y.unique()
(tensor([ True,  True,  True,  ..., False, False, False]),
 tensor([0, 1, 2, 3, 4, 5, 6]))

2. Data Visualization

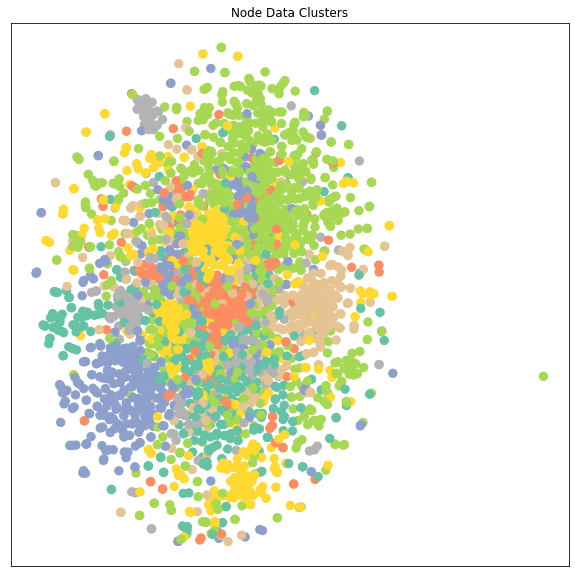
这里简单用TSNE的降维算法把1433 维的node representation降到2维从而来显示每个class的数据的分布, 每种颜色代表一个class。从下面每种颜色的点的分布来看，在学习之前的不同类别的node representation是很难区分开来的，所以很多节点的特征都混在一起

1
2
3
4
5
6
7
8
9
10
11
12
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE

def visualize(h, color,title=""):
    # convert node data x to TSNE embedding data
    z = TSNE(n_components=2).fit_transform(h.detach().cpu().numpy())
    plt.figure(figsize=(10,10))
    plt.xticks([])
    plt.yticks([])
    plt.title(title)
    plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap="Set2")
    plt.show()
1
data.x.shape, data.y.shape
(torch.Size([2708, 1433]), torch.Size([2708]))

1
visualize(data.x,data.y,"Node Data Clusters")

3. 用不同GNN对node embedding进行学习

这里先简单来设计training, testing 的通用函数, 之后尝试用以下不同的模型进行学习和对比:

  • MLP
  • GNN
  • GAT
  • GraphSAGE
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def train(model, criterion, optimizer,data, use_mask=True):
    model.train()
    optimizer.zero_grad()  # Clear gradients.
    out = model(data.x, data.edge_index)  # Perform a single forward pass.
    if use_mask:
        loss = criterion(out[data.train_mask], data.y[data.train_mask])  # Compute the loss solely based on the training nodes.
    else:
        loss = criterion(out, data.y)  # Compute the loss solely based on the training nodes.
    loss.backward()  # Derive gradients.
    optimizer.step()  # Update parameters based on gradients.
    return loss

def test(model, data, use_mask=True):
    model.eval()
    out = model(data.x, data.edge_index)
    pred = out.argmax(dim=1)  # Use the class with highest probability.
    if use_mask:
        test_correct = pred[data.test_mask] == data.y[data.test_mask]  # Check against ground-truth labels.
        test_acc = int(test_correct.sum()) / int(data.test_mask.sum())  # Derive ratio of correct predictions.
    else:
        test_correct = pred == data.y # Check against ground-truth labels.
        test_acc = int(test_correct.sum()) / len(data.y)  # Derive ratio of correct predictions.
    return test_acc

3.1 MLP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import torch
from torch.nn import Linear
import torch.nn.functional as F

class MLP(torch.nn.Module):
    def __init__(self, in_channel, classes, hidden_channels,random_seed=12345):
        super(MLP, self).__init__()
        torch.manual_seed(random_seed)
        self.lin1 = Linear(in_channel, hidden_channels)
        self.lin2 = Linear(hidden_channels, classes)

    def forward(self, x, index):
        x = self.lin1(x)
        x = x.relu()
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.lin2(x)
        return x

model_mlp = MLP(in_channel = dataset.num_features, classes = dataset.num_classes, hidden_channels=16)
optimizer = torch.optim.Adam(model_mlp.parameters(), lr=0.01, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()
print("Model Strucutre:")
print(model_mlp)

for epoch in range(1, 201):
    loss = train(model_mlp, criterion, optimizer,data)
    if epoch%20==0:
        print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')
print()
test_acc = test(model_mlp,data)
print(f'Test Accuracy: {test_acc:.4f}')
Model Strucutre:
MLP(
  (lin1): Linear(in_features=1433, out_features=16, bias=True)
  (lin2): Linear(in_features=16, out_features=7, bias=True)
)
Epoch: 020, Loss: 1.7441
Epoch: 040, Loss: 1.2543
Epoch: 060, Loss: 0.8578
Epoch: 080, Loss: 0.6368
Epoch: 100, Loss: 0.5350
Epoch: 120, Loss: 0.4745
Epoch: 140, Loss: 0.4031
Epoch: 160, Loss: 0.3782
Epoch: 180, Loss: 0.4203
Epoch: 200, Loss: 0.3810

Test Accuracy: 0.5900

1
2


3.2 GCN

GCN Layer 公式如下:

$$
\mathbf{x}_ i^{(k)} = \sum_{j \in \mathcal{N}(i) \cup { i }} \frac{1}{\sqrt{\deg(i)} \cdot \sqrt{\deg(j)}} \cdot ( \mathbf{\Theta} \cdot \mathbf{x}_ j^{(k-1)} ),
$$

这里一些函数定义如下：

  • $\phi(..)$: message函数GCN一样都是linear projection之后用degree进行normalization
  • $\square(..)$ : aggregate 函数用 add
  • $\gamma(..)$: update 函数是直接将aggregate后的结果输出

这里把MLP里面的linear layer换成是GCN layer

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import torch
from torch_geometric.nn import GCNConv
from torch.nn import functional as F

class GCN(torch.nn.Module):
    def __init__(self, in_channel,classes, hidden_channels):
        super(GCN, self).__init__()
        torch.manual_seed(12345)
        self.conv1 = GCNConv(in_channel, hidden_channels)
        self.conv2 = GCNConv(hidden_channels, classes)

    def forward(self, x, edge_index):
        x = self.conv1(x, edge_index)
        x = x.relu()
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.conv2(x, edge_index)
        return x

model_gcn = GCN(in_channel= dataset.num_features, classes= dataset.num_classes, hidden_channels=16)
print("Model Architecture: ")
print(model_gcn)


optimizer = torch.optim.Adam(model_gcn.parameters(), lr=0.01, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()

for epoch in range(1, 201):
    loss = train(model_gcn, criterion, optimizer,data)
    if epoch%20==0:
        print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')
print()
test_acc = test(model_gcn,data)
print(f'Test Accuracy: {test_acc:.4f}')
Model Architecture: 
GCN(
  (conv1): GCNConv(1433, 16)
  (conv2): GCNConv(16, 7)
)
Epoch: 020, Loss: 1.7184
Epoch: 040, Loss: 1.3363
Epoch: 060, Loss: 1.0066
Epoch: 080, Loss: 0.7248
Epoch: 100, Loss: 0.5833
Epoch: 120, Loss: 0.5064
Epoch: 140, Loss: 0.4131
Epoch: 160, Loss: 0.3799
Epoch: 180, Loss: 0.3186
Epoch: 200, Loss: 0.3006

Test Accuracy: 0.8140

1
2


3.3 GAT (Graph Attention Network)

$$
\alpha_ {i,j} = \frac{ \exp(\mathrm{LeakyReLU}(\mathbf{a}^{\top}
[\mathbf{W}\mathbf{h}_ i , \Vert , \mathbf{W}\mathbf{h}_ j]
))}{\sum_ {k \in \mathcal{N}(i) \cup { i }}
\exp(\mathrm{LeakyReLU}(\mathbf{a}^{\top}
[\mathbf{W} \mathbf{h}_ i , \Vert , \mathbf{W}\mathbf{h}_ k]
))}.
$$

节点信息更新
$$
\mathbf{h}_ i^{‘} = \sigma(\frac{1}{K} \sum_ {k=1}^K\sum_ {j \in N(i)} a_{ij}^{k}\mathbf{W}^k\mathbf{h}_ {i})
$$

实际上GAT就是在每个节点把邻居的信息聚合时根据邻居节点的node representation和这个节点的node representation的相似度对聚合的信息有侧重地聚合
其中每个参数的代表:

  • $\mathbf{h}_i$: 节点 i的node representation。这个node representation可以是GNN的某一层的输出
  • $\mathbf{W}$: shared linear transformation. 用于每个节点的共享的线性投映矩阵，所有节点都用相同的W进行投映
  • $k \in \mathcal{N}(i) \cup { i }$: 第i个节点的邻居节点(包括第i个节点本身)。注意因为这里涉及两个sum，两个loop所以计算有点慢
  • $\Vert$: 把两个向量拼接
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import torch
from torch.nn import Linear
import torch.nn.functional as F

from torch_geometric.nn import GATConv

class GAT(torch.nn.Module):
    def __init__(self, in_channel, classes, hidden_channels, dropout_r = 0.2):
        super(GAT, self).__init__()
        torch.manual_seed(12345)
        self.dropout_r = dropout_r
        self.conv1 = GATConv(in_channel, hidden_channels)
        self.conv2 = GATConv(hidden_channels, hidden_channels)
        self.linear = torch.nn.Linear(hidden_channels,classes)

    def forward(self, x, edge_index):
        x = self.conv1(x, edge_index)
        x = x.relu()
        x = F.dropout(x, p=self.dropout_r, training=self.training)
        x = self.conv2(x, edge_index)
        x = self.linear(x)
        return x
    
    
    


model_gat = GAT(in_channel = dataset.num_features, classes = dataset.num_classes, hidden_channels = 16)
optimizer = torch.optim.Adam(model_gat.parameters(), lr=0.01, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()
print("Model Strucutre:")
print(model_gat)

for epoch in range(1, 201):
    loss = train(model_gat, criterion, optimizer,data)
    if epoch%20==0:
        print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')
print()
test_acc = test(model_gat,data)
print(f'Test Accuracy: {test_acc:.4f}')
Model Strucutre:
GAT(
  (conv1): GATConv(1433, 16, heads=1)
  (conv2): GATConv(16, 16, heads=1)
  (linear): Linear(in_features=16, out_features=7, bias=True)
)
Epoch: 020, Loss: 1.5780
Epoch: 040, Loss: 0.5588
Epoch: 060, Loss: 0.1466
Epoch: 080, Loss: 0.0755
Epoch: 100, Loss: 0.0585
Epoch: 120, Loss: 0.0351
Epoch: 140, Loss: 0.0406
Epoch: 160, Loss: 0.0292
Epoch: 180, Loss: 0.0285
Epoch: 200, Loss: 0.0287

Test Accuracy: 0.7230

对GAT做一点调参，提一下性能

  • hidden_channels 用24时比小于16和大于32的时候好
  • dropout=0.8时效果也更好，可能GAT里面的attention的机制容易对一部分特征overfitting
  • epoch设置300更加长些也效果好点
  • 这里调了下参数有了 6% 的提升
1
2
3
4
5
6
7
8
9
10
11
12
13
model_gat = GAT(in_channel = dataset.num_features, classes = dataset.num_classes, hidden_channels = 24, dropout_r= 0.8)
optimizer = torch.optim.Adam(model_gat.parameters(), lr=0.01, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()
print("Model Strucutre:")
print(model_gat)

for epoch in range(1, 301):
    loss = train(model_gat, criterion, optimizer,data)
    if epoch%20==0:
        print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')
print()
test_acc = test(model_gat,data)
print(f'Test Accuracy: {test_acc:.4f}')
Model Strucutre:
GAT(
  (conv1): GATConv(1433, 24, heads=1)
  (conv2): GATConv(24, 24, heads=1)
  (linear): Linear(in_features=24, out_features=7, bias=True)
)
Epoch: 020, Loss: 1.6420
Epoch: 040, Loss: 0.7042
Epoch: 060, Loss: 0.4498
Epoch: 080, Loss: 0.2709
Epoch: 100, Loss: 0.2429
Epoch: 120, Loss: 0.1849
Epoch: 140, Loss: 0.2643
Epoch: 160, Loss: 0.1832
Epoch: 180, Loss: 0.2135
Epoch: 200, Loss: 0.1697
Epoch: 220, Loss: 0.1485
Epoch: 240, Loss: 0.1359
Epoch: 260, Loss: 0.1606
Epoch: 280, Loss: 0.1778
Epoch: 300, Loss: 0.1555

Test Accuracy: 0.7810

1
2


3.4. GraphSAGE (Sample and Aggregate Graph Embedding SAGE)

  • Paper Link: https://arxiv.org/pdf/1706.02216.pdf
  • 其他GNN的node embedding的学习方法都是假设了图里面所有node都是在训练时已经见到的并且有自己的特征数据作为训练集。 而在训练之后，当这些已经见过的node的特征值改变时，可以用GNN对它进行预测。但是实际问题里面，有可能有些node在训练时完全没有见过的(但是出现时会和其他已经见过的node存在link)，因此不能在训练时用这些node的数据进行训练(这个有点像推荐系统的Embedding里面没有见过的userid或itemid的冷启动情况)。GraphSAGE就是用来解决这个问题
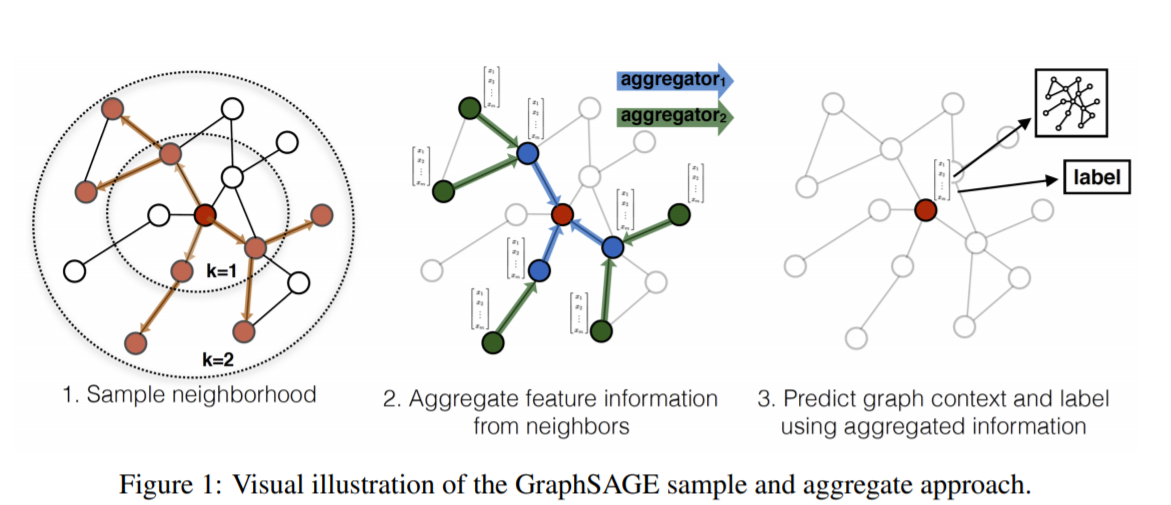
  • GraphSAGE是一种 inductive的representation learning的方法，就是归纳法。它是用于预测之前没有见过的node的embed的ing的特征。它的主要思想是通过学习多个aggregate函数(paper里面提出来mean, LSTM, pooling 三个)，然后这些aggregate函数用neighbor的信息来生成之前没有见过的node的embedding之后再做预测。下面是GraphSAGE的流程图：

  • GraphSAGE 的node embedding的其中一个生成公式为(还有其他用于生成embedding的aggregate函数公式可以参考原文):
    $$
    \mathbf{x}_ {i}^{‘} = \mathbf{W}_ {1}x_{i} + \textbf{mean}_ {j \in N(i)}(\mathbf{x}_{j})
    $$

  • GraphSAGE 的graph-based unsupervised loss function 定义为

$$
\mathbf{J}_ {G}(z_{u}) = -log(\sigma(\mathbf{z}_ {u}^{T}\mathbf{z}_ {v})) - \mathbf{Q} \cdot \mathbf{E}_ {v_ {n} \in P_ {n}(v)}log(\sigma(-\mathbf{z}_ {u}^{T} \mathbf{z}_ {v_{n}}))
$$

其中:

  • $j \in N(i)$ 为第i个节点的第j个neighbor节点

  • $v$ 是和 $u$ 在定长的random walk采样路径出现的节点

  • $Q$ 是负样本的个数， $P_{n}(v)$ 是负采样的分布

  • $z_{u}$是node representation特征

  • 这里$\sigma()$里面计算的是节点和random walk采样时同时出现的其他节点的相似度。相似度越大，loss越小

  • GraphSAGE 的计算embedding算法流程如下:

这里GraphSAGE的基本思路就是

  • 先设定好K (iteration的次数又或者叫search depth搜索的深度)以及初始化没有见过的节点$v$的初始的node embedding
  • 每次遍历时都找到节点 $v$ 的neighbor的nodes并把他们的信息aggregate得到neighbor信息的聚合的embedding
  • 把上一层的$v$ 的embedding和新得到的聚合的neighbor node embedding进行拼接和linear transform得到下一层 node $v$的输出，最后生成之前没见过的node $v$ 的embedding
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import torch
from torch.nn import Linear
import torch.nn.functional as F

from torch_geometric.nn import SAGEConv

class SAGE(torch.nn.Module):
    def __init__(self, in_channel, classes, hidden_channels, dropout_r = 0.2):
        super(SAGE, self).__init__()
        torch.manual_seed(12345)
        self.dropout_r = dropout_r
        self.conv1 = SAGEConv(in_channel, hidden_channels,normalize=True)
        self.conv2 = SAGEConv(hidden_channels, hidden_channels,normalize=True)
        self.linear = torch.nn.Linear(hidden_channels,classes)

    def forward(self, x, edge_index):
        x = self.conv1(x, edge_index)
        x = x.relu()
        x = F.dropout(x, p=self.dropout_r, training=self.training)
        x = self.conv2(x, edge_index)
        x = self.linear(x)
        return x
    
    
    


model_sage = SAGE(in_channel = dataset.num_features, classes = dataset.num_classes, hidden_channels = 24,dropout_r= 0.5)
optimizer = torch.optim.Adam(model_sage.parameters(), lr=0.03, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()
print("Model Strucutre:")
print(model_sage)

for epoch in range(1, 201):
    loss = train(model_sage, criterion, optimizer,data)
    if epoch%20==0:
        print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')
print()
test_acc = test(model_sage,data)
print(f'Test Accuracy: {test_acc:.4f}')
Model Strucutre:
SAGE(
  (conv1): SAGEConv(1433, 24)
  (conv2): SAGEConv(24, 24)
  (linear): Linear(in_features=24, out_features=7, bias=True)
)
Epoch: 020, Loss: 0.3678
Epoch: 040, Loss: 0.0956
Epoch: 060, Loss: 0.0435
Epoch: 080, Loss: 0.0424
Epoch: 100, Loss: 0.1066
Epoch: 120, Loss: 0.0316
Epoch: 140, Loss: 0.0474
Epoch: 160, Loss: 0.0640
Epoch: 180, Loss: 0.1417
Epoch: 200, Loss: 0.0442

Test Accuracy: 0.7800

1
2


3.5 Node Representation Cluster Visualization

1
2
3
4
5
6
models = {"MLP":model_mlp, "GCN":model_gcn,"GAT":model_gat, "GraphSAGE":model_sage}
for k in models.keys():
    model = models[k]
    out = model(data.x, data.edge_index)
    title = f"Node Representation learned by {k}"
    visualize(out, data.y, title)

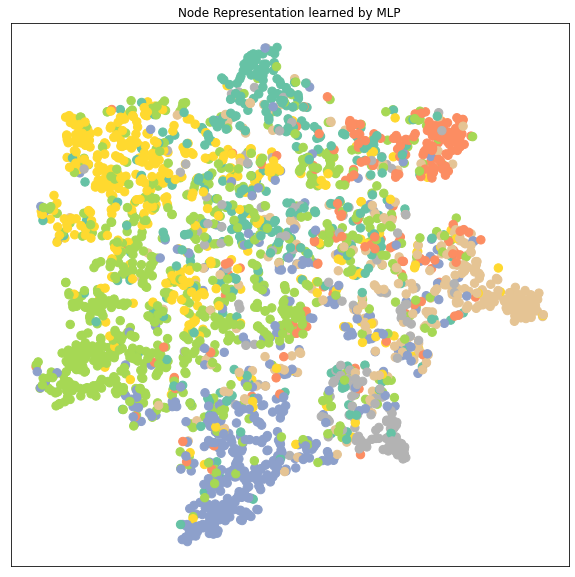
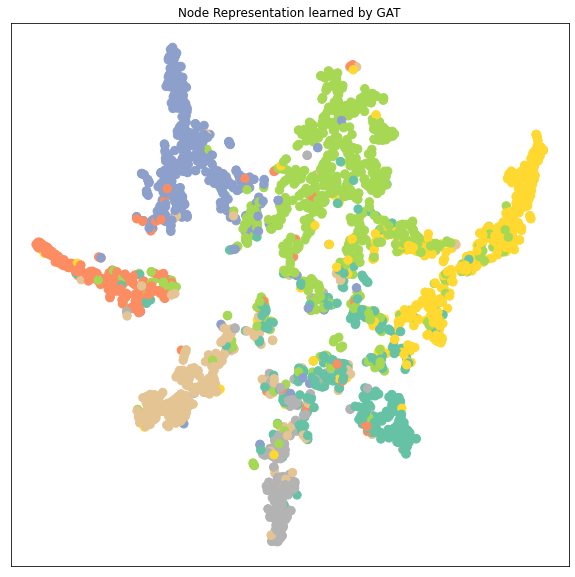
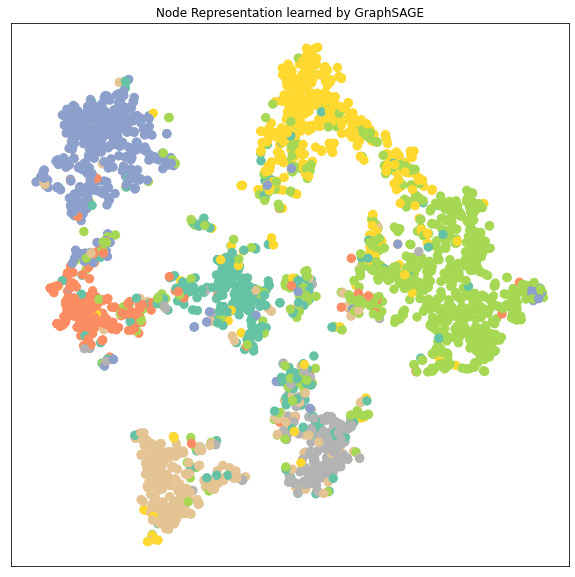
从降维后的 node embedding的cluster的分布来分析不同模型的性能:

  • 可以看到GCN, GAT, GraphSAGE 的node embedding的7个clusters都比MLP要区分得清楚，即每个类的特征差异较大容易被识别出来所以GNN都比MLP要好
  • GAT和GraphSAGE的clusters之间的距离都比GCN的clusters之间的距离要远，特别是GAT。GAT的每个cluster都收缩成一束一束的聚合起来。而因为这里显示的cluster是data.x样本，包括了训练集在内，所以cluster区分得越明显很有可能是数据拟合得很好甚至是有overfitting的可能。
1
2


4. Assignment

4.1 Dataset选择

  • Pubmed: https://arxiv.org/abs/1603.08861
    这个数据集合Cora一样: Nodes represent documents and edges represent citation links
  • Citeseer: https://arxiv.org/abs/1603.08861
    这个数据集合Cora一样: Nodes represent documents and edges represent citation links
  • CitationFull： https://arxiv.org/abs/1707.03815
    Nodes represent documents and edges represent citation links.
  • 本来想尝试其他数据，但是其他数据集太大训练起来很慢，后期有时间再试试看

这里写个函数一次性打印所有要用的dataset的信息，看一下不同dataset的node， edge信息，并用table打印出来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# dataset used by GAT
from torch_geometric.datasets import PPI, Reddit,NELL,QM7b,CitationFull,AMiner
pubmed_dataset = Planetoid(root='./dataset', name='Pubmed', transform=NormalizeFeatures())
Citeseer_dataset = Planetoid(root='./dataset', name='CITESEER', transform=NormalizeFeatures())
CitationFull_dataset =CitationFull(root='./dataset',name="DBLP",transform=NormalizeFeatures())
# PPI_train = PPI(root='./dataset',  split='train',transform=NormalizeFeatures())
# PPI_test = PPI(root='./dataset',  split='test',transform=NormalizeFeatures())
# PPI_dataset = {'train':PPI_train,"test":PPI_test}


# AMiner_dataset = AMiner(root='./dataset',transform=NormalizeFeatures())
#QM7b_dataset = QM7b(root='./dataset', transform=NormalizeFeatures())
# Reddit_dataset = Reddit(root='./dataset', transform=NormalizeFeatures())
# NELL_dataset = NELL(root='./dataset', transform=NormalizeFeatures())
Downloading https://data.dgl.ai/dataset/ppi.zip
Extracting dataset/ppi.zip

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import pandas as pd
#mydatasets = {"Pubmed":pubmed_dataset, "Citeseer":Citeseer_dataset, "Reddit":Reddit_dataset,"NELL":NELL_dataset}
mydatasets = {"CitationFull":CitationFull_dataset,"Pubmed":pubmed_dataset, "Citeseer":Citeseer_dataset}
df = pd.DataFrame(columns={"dataset","#graphs","#features","#classes"})

dic = {"dataset":[],"#graphs":[],"#features":[],"#classes":[],"#nodes":[],"#edges":[],"Has_isolated_nodes":[],"undirected":[]}
for k in mydatasets.keys():
    tmp = {k:mydatasets[k]}
    if k in ["PPI"]:
        tmp = mydatasets[k]
    for key in tmp.keys():
        dataset = tmp[key]
        print("dataset: ",key)
        dic['dataset'].append(key)
        dic['#graphs'].append(len(dataset))
        dic['#features'].append(dataset.num_features)
        dic['#classes'].append(dataset.num_classes)
        data = dataset[0]
        dic['#nodes'].append(data.num_nodes)
        dic['#edges'].append(data.num_edges)
        dic['Has_isolated_nodes'].append(data.contains_isolated_nodes())
        dic['undirected'].append(data.is_undirected())

data_stat = pd.DataFrame(dic)
data_stat.T

# print()
# print(f'Dataset: {dataset}:')
# print('======================')
# print(f'Number of graphs: {len(dataset)}')
# print(f'Number of features: {dataset.num_features}')
# print(f'Number of classes: {dataset.num_classes}')

# data = dataset[0]  # Get the first graph object.

# print()
# print(data)
# print('======================')

# # Gather some statistics about the graph.
# print(f'Number of nodes: {data.num_nodes}')
# print(f'Number of edges: {data.num_edges}')
# print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}')
# print(f'Number of training nodes: {data.train_mask.sum()}')
# print(f'Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}')
# print(f'Contains isolated nodes: {data.contains_isolated_nodes()}')
# print(f'Contains self-loops: {data.contains_self_loops()}')
# print(f'Is undirected: {data.is_undirected()}')
dataset:  CitationFull
dataset:  Pubmed
dataset:  Citeseer

0 1 2
dataset CitationFull Pubmed Citeseer
#graphs 1 1 1
#features 1639 500 3703
#classes 4 3 6
#nodes 17716 19717 3327
#edges 105734 88648 9104
Has_isolated_nodes False False True
undirected True True True 
1
2
# KarateClub_dataset[0]
# ! du -h ./dataset/

4.2 GNN Model Training

这里写个一次性训练所有模型和训练集的函数，并把所有模型的结果打印

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
models = {}

def train_models(models, datasets):
    res = {}
    mymodels = {}
    for key in datasets.keys():
        if key in ["CitationFull"]:
            dataset = datasets[key]
            testset = datasets[key]
        else:
            dataset = datasets[key]
            testset= None
        data = dataset[0]
        if key not in res.keys():
            res[key] = {}
        if key not in models.keys():
            mymodels[key] = {}
            
        model_mlp2 = MLP(in_channel = dataset.num_features, classes = dataset.num_classes,hidden_channels=16)
        model_gcn2 = GCN(in_channel = dataset.num_features, classes = dataset.num_classes,hidden_channels=16)
        model_sage2 = SAGE(in_channel = dataset.num_features, classes = dataset.num_classes,hidden_channels = 24,dropout_r= 0.5)
        model_gat2 = GAT(in_channel = dataset.num_features, classes = dataset.num_classes,hidden_channels = 24, dropout_r= 0.8)
        models = {"MLP":model_mlp2, "GCN":model_gcn2,"GAT":model_gat2, "GraphSAGE":model_sage2}
        mymodels[key] = models
        for name, model in models.items():
            if name not in res[key].keys():
                res[key][name] =None    
            print(f"Dataset: {key}, model: {name}")
            optimizer = torch.optim.Adam(model.parameters(), lr=0.03, weight_decay=5e-4)
            criterion = torch.nn.CrossEntropyLoss()
            #print("Model Strucutre:")
            #print(model)
            for epoch in range(1, 201):
                use_test_mask = True if testset== None else False
                loss = train(model, criterion, optimizer,data,use_test_mask)
                if epoch%20==0:
                    print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')
            print()
            use_test_mask = True if testset== None else False
            test_acc = test(model,data,use_test_mask)
            print(f'Test Accuracy: {test_acc:.4f}')
            res[key][name] = test_acc
    return pd.DataFrame(res), mymodels
1
2
test_results, trained_models = train_models(models, mydatasets)
test_results
Dataset: CitationFull, model: MLP
Epoch: 020, Loss: 0.9961
Epoch: 040, Loss: 0.8182
Epoch: 060, Loss: 0.7515
Epoch: 080, Loss: 0.7192
Epoch: 100, Loss: 0.6986
Epoch: 120, Loss: 0.6905
Epoch: 140, Loss: 0.6799
Epoch: 160, Loss: 0.6746
Epoch: 180, Loss: 0.6669
Epoch: 200, Loss: 0.6673

Test Accuracy: 0.8128
Dataset: CitationFull, model: GCN
Epoch: 020, Loss: 0.7686
Epoch: 040, Loss: 0.5725
Epoch: 060, Loss: 0.5072
Epoch: 080, Loss: 0.4807
Epoch: 100, Loss: 0.4712
Epoch: 120, Loss: 0.4601
Epoch: 140, Loss: 0.4548
Epoch: 160, Loss: 0.4475
Epoch: 180, Loss: 0.4489
Epoch: 200, Loss: 0.4439

Test Accuracy: 0.8606
Dataset: CitationFull, model: GAT
Epoch: 020, Loss: 0.7240
Epoch: 040, Loss: 0.5830
Epoch: 060, Loss: 0.4896
Epoch: 080, Loss: 0.4724
Epoch: 100, Loss: 0.4547
Epoch: 120, Loss: 0.4440
Epoch: 140, Loss: 0.4313
Epoch: 160, Loss: 0.4150
Epoch: 180, Loss: 0.4025
Epoch: 200, Loss: 0.3877

Test Accuracy: 0.8818
Dataset: CitationFull, model: GraphSAGE
Epoch: 020, Loss: 0.4138
Epoch: 040, Loss: 0.2719
Epoch: 060, Loss: 0.2323
Epoch: 080, Loss: 0.2151
Epoch: 100, Loss: 0.2272
Epoch: 120, Loss: 0.1943
Epoch: 140, Loss: 0.2020
Epoch: 160, Loss: 0.1900
Epoch: 180, Loss: 0.1968
Epoch: 200, Loss: 0.2002

Test Accuracy: 0.9690
Dataset: Pubmed, model: MLP
Epoch: 020, Loss: 0.4589
Epoch: 040, Loss: 0.1964
Epoch: 060, Loss: 0.1649
Epoch: 080, Loss: 0.1044
Epoch: 100, Loss: 0.0887
Epoch: 120, Loss: 0.1578
Epoch: 140, Loss: 0.1371
Epoch: 160, Loss: 0.1269
Epoch: 180, Loss: 0.1296
Epoch: 200, Loss: 0.1131

Test Accuracy: 0.7280
Dataset: Pubmed, model: GCN
Epoch: 020, Loss: 0.5874
Epoch: 040, Loss: 0.2958
Epoch: 060, Loss: 0.2396
Epoch: 080, Loss: 0.1658
Epoch: 100, Loss: 0.1735
Epoch: 120, Loss: 0.1848
Epoch: 140, Loss: 0.1198
Epoch: 160, Loss: 0.1091
Epoch: 180, Loss: 0.1549
Epoch: 200, Loss: 0.1069

Test Accuracy: 0.7930
Dataset: Pubmed, model: GAT
Epoch: 020, Loss: 0.3768
Epoch: 040, Loss: 0.1317
Epoch: 060, Loss: 0.1555
Epoch: 080, Loss: 0.2786
Epoch: 100, Loss: 0.1570
Epoch: 120, Loss: 0.1774
Epoch: 140, Loss: 0.0932
Epoch: 160, Loss: 0.1104
Epoch: 180, Loss: 0.0623
Epoch: 200, Loss: 0.0201

Test Accuracy: 0.7140
Dataset: Pubmed, model: GraphSAGE
Epoch: 020, Loss: 0.0753
Epoch: 040, Loss: 0.0226
Epoch: 060, Loss: 0.0557
Epoch: 080, Loss: 0.0116
Epoch: 100, Loss: 0.0086
Epoch: 120, Loss: 0.0297
Epoch: 140, Loss: 0.0106
Epoch: 160, Loss: 0.0835
Epoch: 180, Loss: 0.0064
Epoch: 200, Loss: 0.0906

Test Accuracy: 0.7700
Dataset: Citeseer, model: MLP
Epoch: 020, Loss: 1.1613
Epoch: 040, Loss: 0.5621
Epoch: 060, Loss: 0.4475
Epoch: 080, Loss: 0.4112
Epoch: 100, Loss: 0.3795
Epoch: 120, Loss: 0.3416
Epoch: 140, Loss: 0.3785
Epoch: 160, Loss: 0.3341
Epoch: 180, Loss: 0.3596
Epoch: 200, Loss: 0.4045

Test Accuracy: 0.5910
Dataset: Citeseer, model: GCN
Epoch: 020, Loss: 1.3142
Epoch: 040, Loss: 0.8198
Epoch: 060, Loss: 0.5696
Epoch: 080, Loss: 0.4871
Epoch: 100, Loss: 0.4850
Epoch: 120, Loss: 0.4268
Epoch: 140, Loss: 0.3961
Epoch: 160, Loss: 0.3845
Epoch: 180, Loss: 0.3508
Epoch: 200, Loss: 0.3517

Test Accuracy: 0.7010
Dataset: Citeseer, model: GAT
Epoch: 020, Loss: 0.7527
Epoch: 040, Loss: 0.4082
Epoch: 060, Loss: 0.4495
Epoch: 080, Loss: 0.4963
Epoch: 100, Loss: 0.3861
Epoch: 120, Loss: 0.2898
Epoch: 140, Loss: 0.3495
Epoch: 160, Loss: 0.2082
Epoch: 180, Loss: 0.2877
Epoch: 200, Loss: 0.3382

Test Accuracy: 0.6530
Dataset: Citeseer, model: GraphSAGE
Epoch: 020, Loss: 0.3369
Epoch: 040, Loss: 0.1300
Epoch: 060, Loss: 0.0721
Epoch: 080, Loss: 0.0956
Epoch: 100, Loss: 0.1785
Epoch: 120, Loss: 0.0476
Epoch: 140, Loss: 0.0424
Epoch: 160, Loss: 0.0556
Epoch: 180, Loss: 0.1063
Epoch: 200, Loss: 0.0645

Test Accuracy: 0.6720

CitationFull Pubmed Citeseer
MLP 0.812768 0.728 0.591
GCN 0.860634 0.793 0.701
GAT 0.881802 0.714 0.653
GraphSAGE 0.969011 0.770 0.672

Conclusion

  • 和以往的像图片文本之类的数据不同，图的数据的训练的不同点有下面几个
    • 除了要输入节点的数据特征外，还要输入edge作为关联的数据。
    • 另外GNN在训练时是可以同时更新多个不同node的embedding。
    • GNN训练时更加像NLP的训练方法，都是把一部分的node（在NLP里面是word token）mask掉并对这部分内容(node或者link)预测
    • 另外在node classification里面因为GNN输入是图，输出也是转换后学习后的图(图里的每个node的值代表这个node所属的class)，可以一下子把所有要预测的node进行预测。不过也可以通过mask的形式在图里面采样进行分batch训练
  • 另外在上面实验中可以看到，在相同配置中GCN要把GAT和GraphSAGE好，GAT比较容易overfit，而GAT和GraphSAGE训练相对于GCN比较慢因为在训练node embedding时设计到两个循环。不过GAT，GraphSAGE相对于GCN训练时的loss收敛得很快。就目前的任务来看感觉GCN比GAT，GraphSAGE要好，但是可能不同的任务模型用起来效果也不一样
  • 当node embedding训练得好的时候，不同的类的node embedding特征很容易被区别开来，相同类的node的特征会内聚而不同类的特征会远离，这个其实和普通的NN分类器里面提取的特征一样，比较正常。

Reference

#

Comments

Links

Categories

Tags

Amdahl's Law1
Backpropagation1
Bagging1
BeautifulSoup1
Binary Tree1
Blending1
Boosting1
Boosting Machine1
BuckSort1
C++1
Collaborative Filtering1
Confusion Metric1
Convolution Neural Network1
Cross Validation1
D3.js1
DCN1
DIN1
Data Analysis1
Data Mining2
Data Visualization1
Datawhale Team Learning2
DeepFM1
Dropout1
EGES1
Ensemble Learning6
FFM Model1
GATE1
GNN8
Graph8
Graph Embedding1
Holdout1
Hypothesis Test1
Independence Test1
Installation1
JavaScript1
K-Mean Clustering1
KMean Clustering1
LGBM2
Machine Learning1
Markdown1
Model Evaluation1
Model Selection1
Natural Language Representations1
Nature Language Processing1
Negative Sampling1
NeuralFM1
P-value1
Parallel Computing1
Parallel Speedup1
PySpark1
ROC curve1
Recommendation System1
Regression1
Regular Expression1
Scala1
Shell Tutorial1
Sorting1
Spark1
Stacking2
Swing1
Traversal1
Tutorial1
Unsupervised Learning1
Variable Selection1
WSDM1
Web Scrapping1
Wide and Deep1
Wide and Deep Model1
Wide&Deep Model1
Word Embedding1
Word vector1
binary search1
bubble sort1
commands1
insertion sort1
merge sort1
non-parametric learning1
quick sort1
review1
statistic analytics tool1

Recent

Archives

Subscribe to Updates

Follow
×