Recommendation-System-GATE

Background

这篇文章介绍了来自麦吉尔大学(McGrill University) Chen Ma 等人在 2019 WSDM发表的文章: Gated-Attentive Autoencoder for Content-Aware Recommendation (GATE). 文章链接看这里: Link.
我的Google Slide PPT介绍可以看这里 Slide

Motivation

在推荐系统里面随着用户和商品的急速增长， 个性化推荐系统这篇文章考虑了以下两个问题:

1. 一些稀疏的隐性反馈信息利用困难。 比如一个用户喜欢一个商品， 而这个商品在内容上面(比如文字描述信息等)和这个被买的商品很相似，那么这个商品就也很有可能会被买。另外，像用1来标记用户喜欢，0来标记用户不喜欢或者没评分这种稀疏的评分方式也可能有一些隐性反馈可以挖掘。
2. 不同类型的数据的结合使用困难。比如像是文本描述数据和0或者1的评分标签两种不同类型的数据要同时结合起来让模型学习，需要把各自的隐性特征(hidden representation)通过一定方式结合起来使用。

而这篇文章为了解决这两个问题，主要从模型的结构入手，并提出创新的结构。这篇文章的主要贡献有以下:

1. 提出一种word-attention module 去捕捉item的文本特征的各个单词的重要性。把重要的单词特征进行提取和融合
2. 提出一种 neural gating layer去自动把rating的hidden representation和 word attention module学到的embedding进行自动融合得到当前item的hidden representation。
3. 它也假设了用户如果对一个item的neighbor 的item内容感兴趣，也会对这个item内容感兴趣。所以也提出一种基于item-item 关系的neighbor-attention layer把相邻的item的信息也考虑进来。
4. 这个模型的word-attention的layer是可以可视化并且解释的。

Gated-Attentive Autoencoder for Content-Aware Recommendation

Formulation

这里我们先来定义一些参数和输入:

• R: m-by-n binary user preferences matrix. Rij = 1 -> user prefers.
• ri : binary rating of the ith item in matrix R
• D: The entire collection of n items is represented by a list of documents D. Di is the ith item content, represented by a sequence of words.
• N: n-by-n item binary adjacency matrix. Nij = 1 means item i and j are connected (neighbor)

Loss

首先这个模型是要把稀疏的rating matrix R进行预测把为0的entry的进行rating的预测和填充，这个就像是矩阵分解里面把稀疏矩阵变成dense matrix一样。而使用的loss 就是基于Auto-encoder 的loss改进得到的:

加了Regularization term后， loss变成:

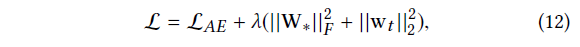
Model Architecture

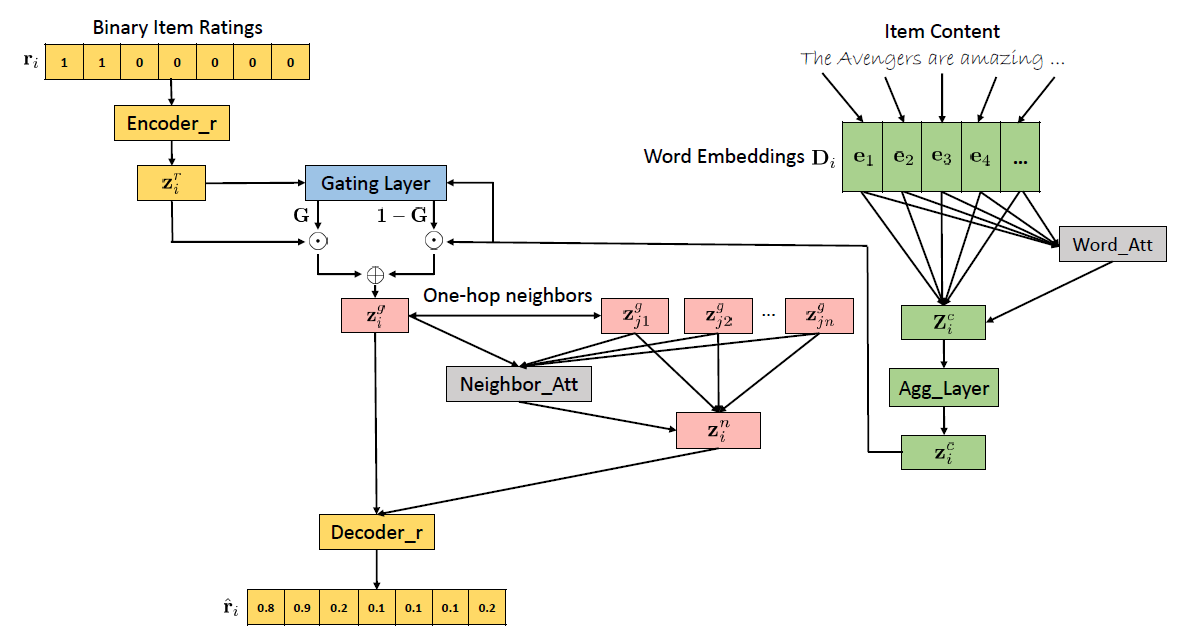
GATE的架构如下， 他有4种不同模块组成(分别对应不同的颜色)。黄色代表encoder-decoder模型， 绿色代表word-attention 模块， 蓝色代表Neural Gating layer, 红色代表neighbor-attention layer

Encoder and Decoder

首先encoder和decoder的模块里面， encoder 模块先通过两层的MLP对binary rating进行encoding得到隐性信息。这个有点像矩阵分解(Matrix Factorization)里面从稀疏的binary rating得到item的embedding一样。

其中ri代表第i个item的rating，每个值代表一个user的评价。1代表user 喜欢这个item。而0代表没有评分。所以这个ri是一个multi-onehot vector

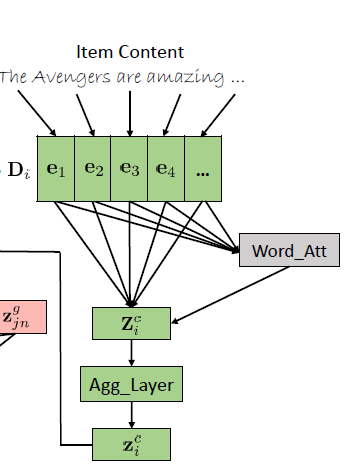
Word Attention

在word attention 模块， 它的目标是要把item的文本描述里面的多个重要的单词进行提取和学习，因此为了提取分散在不同位置的重要的单词，这里用了attention机制进行学习。
它的步骤如下:
先计算Attention matrix：
$$
A_ {i} = \text{softmax}(\mathbf{W}_ {a1} tanh(\mathbf{W}_ {a2} \mathbf{D}_ i + \mathbf{b}_ {a2}) + b_ {a1} )
$$

然后计算hidden representation matrix $\mathbf{Z}_ i ^c$, 这个矩阵的每一列代表一个做了attention之后的单词的embedding:

$$
\mathbf{Z}_ i ^c = \mathbf{A}_ i D_ i ^T
$$

最后我们将每个word embedding通过乘上一个learnable的weight 系数并将所有word embedding相加进行学习得到最后content的embedding， 即
$$
\mathbf{z}_ i^c = a_ t (\mathbf{Z}_ i^{c^T} w_t)
$$

这里的$w_t$ 就是一个weight column vector对每个word embedding权重相加。

Neural Gating Layer

在GATE里面的Neural Gating layer 参考了LSTM里面的相加的layer通过一个自适应的系数G对模型的rating embedding和 content embedding权重进行相加和信息融合。公式如下:
$$
\mathbf{G} = \text{sigmoid}(\mathbf{W}_ {g1}z_ {i}^{r} + \mathbf{W}_ {g2}z_ {i}^{c} + b_ g) \\
z_ i^g = G \cdot z_ i^r + (1-G) \cdot z_ i ^c
$$

其中上标为c的代表item content的embedding对应的参数 而上标为r的代表item binary rating的embedding对应的参数.

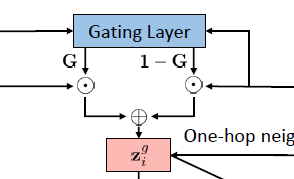
这里虽然说是把不同的embedding的信息进行融合，但是因为信息的来源不一样，有可能每个值所代表的隐性信息代表的含义也不一样，这样直接相加的话还是感觉有些牵强。比起这个方式的信息融合， 我更加倾向于把embedding拼接然后做linear projection的方法. 而G是一个scalar value系数对两边的embedding的信息进行权衡。

Neighbor Attention layer

Neighbor Attention layer 是设计是基于一个假设: 用户对一个item的喜欢可以从这个用户对这个item的相关临近的item的喜欢里面看出。如果这个用户喜欢这个item的neighborhood里面的item，那么用户也有可能喜欢这个item。
这一层的layer结构如下：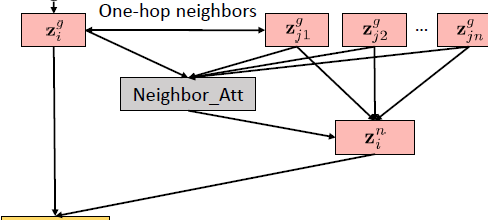

所以在做完这个item的hidden representation计算得到$z_ i^g$ 后我们可以根据之前的adjacency matrix N 找到这个item的neighborhood里面的item。而这个adjacency matrix的搭建是根据rating matrix R计算item和item之间的相似度，再通过threshold取值得到， 原文是这么说的:
For items that do not inherently have item-item relations, we can compute the item-itemsimilarity from the binary rating matrix R and set a threshold to select neighbors.

而这一层的计算公式如下:

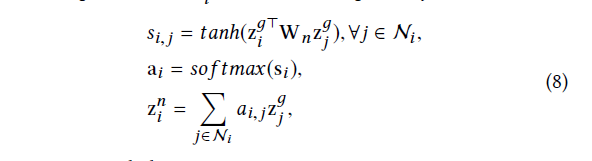
Visualization of important word

这篇文章最后的创新点就是它可以通过学习到的 word attention的attention matrix $A_ i$ 对重要单词进行可视化。首先$A_ i$ matrix每一列代表了一个单词的重要性系数， 然后把 $A_ i \in R^{da \times li}$ 通过把每一个row 进行相加得到$a_ i \in R^{li}$的 vector，而这个vector每个值代表那个单词的重要性。

Experiments

Metrics

这里paper用的metrics有两个:

• Recall@k (R@k)
  $Recall @ k = \frac{\text{num of relevant recommended top K}}{ \text{ num of user prefers}}$.
  For each user, Recall@k (R@k) indicates what percentage of her rated
  items can emerge in the top k recommended items.
  top-K的Recall随着k越大 对用户喜欢的item的命中率越高，recall越大

• NDCG@k (N@k) is the normalized discounted cumulative gain at k. It measures of ranking quality. (how relevant the recommended top k elements are)
  NDCG 测量推荐的商品和用户的相关度。top-K的NDCG随着k越大 越有可能推和用户无关的东西，那么NDCG就越小。计算公式如下: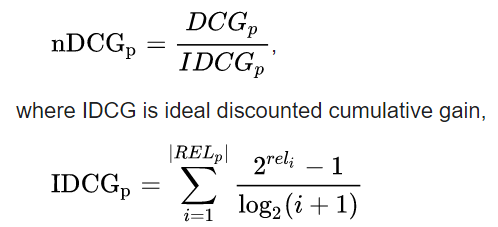

  

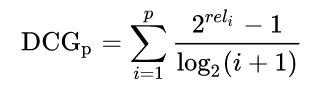
下面 是其中一部分用于不同数据集的对比实验。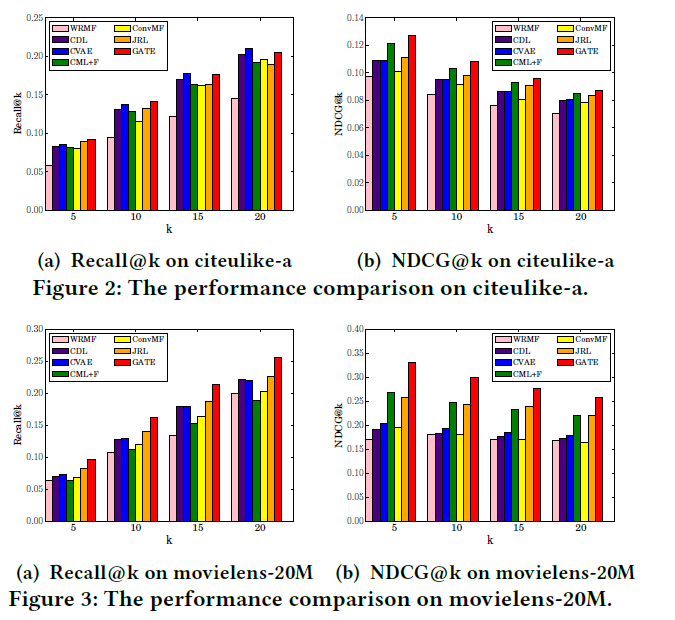

Comparison

下面是对不同模型在同一个k设定下的实验: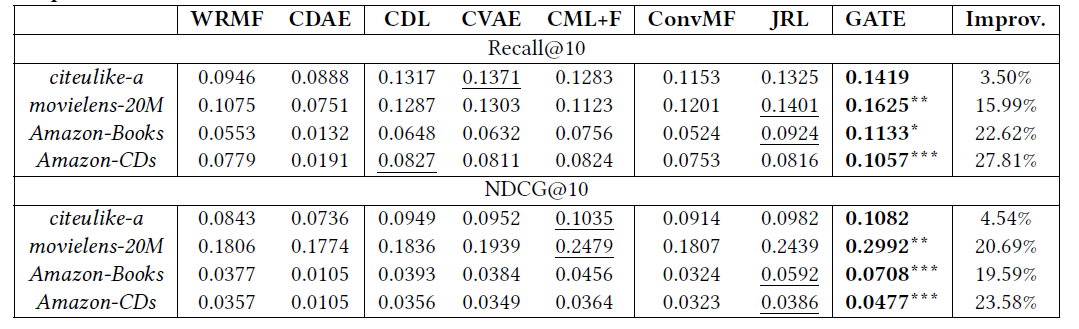

Hyper-parameter Tuning

下面是对loss里面的confidence 系数$p$和 word attention embedding的大小 da的效果实验. 原文里面$p$ 选取了20， da选取50.不同不同数据集有不同的设定，这个可以看看原文。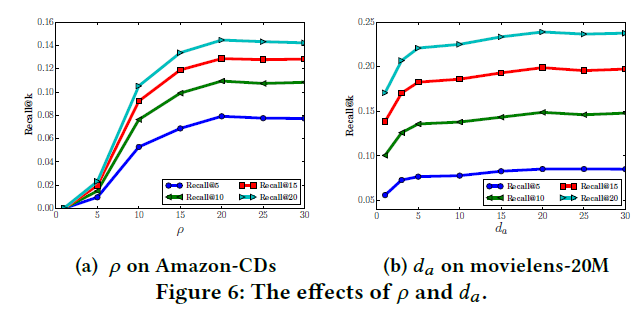

Source Code

Github source code: https://github.com/allenjack/GATE/blob/master/run.py

import torch
from torch.autograd import Variable
import torch.nn.functional as F

if torch.cuda.is_available():
    import torch.cuda as T
else:
    import torch as T


class GATE(torch.nn.Module):
    def __init__(self, num_users, num_items, num_words, H, drop_rate=0.5, att_dim=20):
        """
        In the constructor we instantiate two nn.Linear modules and assign them as
        member variables.
        """
        super(GATE, self).__init__()
        self.H = H[1]
        self.drop_rate = drop_rate
        if torch.cuda.is_available():
            self.item_gated_embedding = torch.nn.Embedding(
                num_embeddings=num_items + 1,
                embedding_dim=self.H,
                padding_idx=num_items  # the last item index is the padded index
            ).cuda()
            self.item_gated_embedding.weight.requires_grad = False

            self.word_embedding = torch.nn.Embedding(
                num_embeddings=num_words + 1,
                embedding_dim=self.H,
                padding_idx=num_words  # the last word index is the padded index
            ).cuda()

            self.aggregation = torch.nn.Linear(att_dim, 1).cuda()
            self.att1 = torch.nn.Linear(self.H, self.H).cuda()
            self.att2 = torch.nn.Linear(self.H, att_dim).cuda()

            self.linear1 = torch.nn.Linear(num_users, H[0]).cuda()
            self.linear2 = torch.nn.Linear(H[0], H[1]).cuda()
            self.linear3 = torch.nn.Linear(H[1], H[2]).cuda()
            self.linear4 = torch.nn.Linear(H[2], num_users).cuda()

        else:
            self.item_gated_embedding = torch.nn.Embedding(
                num_embeddings=num_items + 1,
                embedding_dim=self.H,
                padding_idx=num_items  # the last item index is the padded index
            )
            self.item_gated_embedding.weight.requires_grad = False

            self.word_embedding = torch.nn.Embedding(
                num_embeddings=num_words + 1,
                embedding_dim=self.H,
                padding_idx=num_words  # the last word index is the padded index
            )

            self.aggregation = torch.nn.Linear(att_dim, 1)
            self.att1 = torch.nn.Linear(self.H, self.H)
            self.att2 = torch.nn.Linear(self.H, att_dim)

            self.linear1 = torch.nn.Linear(num_users, H[0])
            self.linear2 = torch.nn.Linear(H[0], H[1])
            self.linear3 = torch.nn.Linear(H[1], H[2])
            self.linear4 = torch.nn.Linear(H[2], num_users)

        self.neighbor_attention = Variable(torch.zeros(self.H, self.H).type(T.FloatTensor), requires_grad=True)
        self.neighbor_attention = torch.nn.init.xavier_uniform_(self.neighbor_attention)

        # G = sigmoid(gate_matrix1 \dot item_embedding + gate_matrix2 \dot item_context_embedding + bias)
        self.gate_matrix1 = Variable(torch.zeros(self.H, self.H).type(T.FloatTensor), requires_grad=True)
        self.gate_matrix2 = Variable(torch.zeros(self.H, self.H).type(T.FloatTensor), requires_grad=True)
        self.gate_matrix1 = torch.nn.init.xavier_uniform_(self.gate_matrix1)
        self.gate_matrix2 = torch.nn.init.xavier_uniform_(self.gate_matrix2)
        self.gate_bias = Variable(torch.zeros(1, self.H).type(T.FloatTensor), requires_grad=True)
        self.gate_bias = torch.nn.init.xavier_uniform_(self.gate_bias)

    def forward(self, batch_item_index, batch_x, batch_word_seq, batch_neighbor_index):
        z_1 = F.tanh(self.linear1(batch_x))
        # z_1 = F.dropout(z_1, self.drop_rate)

        z_rating = F.tanh(self.linear2(z_1))
        z_content = self.get_content_z(batch_word_seq)

        gate = F.sigmoid(z_rating.mm(self.gate_matrix1) + z_content.mm(self.gate_matrix2) + self.gate_bias)
        gated_embedding = gate * z_rating + (1 - gate) * z_content

        # save the embedding for direct lookup
        self.item_gated_embedding.weight[batch_item_index] = gated_embedding.data

        gated_neighbor_embedding = self.item_gated_embedding(batch_neighbor_index)

        # aug_gated_embedding: [256, 1, 50]
        aug_gated_embedding = torch.unsqueeze(gated_embedding, 1)
        score = torch.matmul(aug_gated_embedding, torch.unsqueeze(self.neighbor_attention, 0))
        # score: [256, 1, 480]
        score = torch.bmm(score, gated_neighbor_embedding.permute(0, 2, 1))

        # make the 0 in score, which will make a difference in softmax
        score = torch.where(score == 0, T.FloatTensor([float('-inf')]), score)
        score = F.softmax(score, dim=2)
        # if the vectors all are '-inf', softmax will generate 'nan', so replace with 0
        score = torch.where(score != score, T.FloatTensor([0]), score)
        gated_neighbor_embedding = torch.bmm(score, gated_neighbor_embedding)
        gated_neighbor_embedding = torch.squeeze(gated_neighbor_embedding, 1)

        # gated_embedding = F.dropout(gated_embedding, self.drop_rate)
        # gated_neighbor_embedding = F.dropout(gated_neighbor_embedding, self.drop_rate)

        z_3 = F.tanh(self.linear3(gated_embedding))
        # z_3 = F.dropout(z_3, self.drop_rate)
        z_3_neighbor = F.tanh(self.linear3(gated_neighbor_embedding))
        # z_3_neighbor = F.dropout(z_3_neighbor, self.drop_rate)

        y_pred = F.sigmoid(self.linear4(z_3) + z_3_neighbor.mm(self.linear4.weight.t()))

        return y_pred

    def get_content_z(self, batch_word_seq):
        # [batch_size, num_word, hidden_dim], e.g., [256, 300, 100]
        batch_word_embedding = self.word_embedding(batch_word_seq)
        score = F.tanh(self.att1(batch_word_embedding))
        score = F.tanh(self.att2(score))
        # score dimension: [256, 300, 20]
        score = F.softmax(score, dim=1)
        # permute to make the matrix as [256, 50, 176]
        matrix_z = torch.bmm(batch_word_embedding.permute(0, 2, 1), score)
        linear_z = self.aggregation(matrix_z)
        linear_z = torch.squeeze(linear_z, 2)
        z = F.tanh(linear_z)

        return z

Reference

[1] Paper： https://arxiv.org/abs/1812.02869
[2] Github: https://github.com/allenjack/GATE
[3] 我知乎的博客: https://zhuanlan.zhihu.com/p/390923011