NLP Word Representations

1. Representation:

1.1 WordNet

a thesaurus containing lists of synonyms and hpernyms, using “is-a” to denote the relationship among words.

• Advantages:

  • easy to understand the relationship. It is interpretable.

• Disadvantages:

  • good as resource, but missing nuance in different context. Eg: “proficient” doesn’t always mean “good”
  • Hard to update with new meanings of words, since the meanings of words may change along time
  • subjective and bias
  • Require Human to label
  • Can’t compute accurate word similarity
    

1.2 One-hot

Represent word as discrete symbol, eg. 0 or 1
Example: In sentence “I like dog”, the vector for “I” =[1,0,0], the vector for “like” =[0,1,0],the vector for “dog” =[0,0,1]

word	one-hot vector
“I”	1 0 0
“like”	0 1 0
“Dog”	0 0 1

Note:

1. Usually, the number of of vocabulary is equal to the number of entry in the one-hot vector. This enables the (Manhatton) distance between any two words/labels is same and the feature of each word is independent with each other.
   The feature of a word contains no information about another word and hence don’t affect other words. Moreover, this method also has physical meaning and easy to understand.
   For example:
   Assume in linear regression,
   we have $y =w_1x_1 + w_2x_2 + w_3x_3 $, in vector representation it is $Y = [w_1, w_2, w_3] \cdot [x_1, x_2, x_3]^T = WX$
   Let vector X be a one-hot vector. That is, one of $x_1, x_2, x_3$ must be one. In this case, $WX$ becomes a lookup table to choose which weight $w_1, w_2, w_3$ should be learned. In this case, weight $w_1$ is affected by feature $x_1$ only, without being affected other features. This can lead to faster convergence of $w_1$ in learning .

• Advantage:
  • able to represent words into number for computing
  • Easy to understand, since it has physical meaning
  • Features/ labels are independent from each other
• Disadvantage:
  • Vector dimension equal to the number of words in vocabulary, it could be very big
  • No natural notion of similarity, since word vectors are orthogonal.
  • Hard to extend the representation of labels when more labels are added.
  • Could be memory expensive when a large group of labels involved. Eg, represent vocabulary in a book as one-hot vector, the vectors could be very large and sparse.
    

1.3 Bag of Words (BOW)

Similar to one-hot, it represents each word as orthogonal vector, but the number of vector is the frequency the word appears. In BOW, a text (such as a sentence or a document) is represented as the bag (multiset)/set of its words, disregarding grammar and even word order but keeping multiplicity.

• Advantage:
  • Easy to realize and compute
  • Easy to use for simple case (the order of words don’t matter a lot)
• Disadvantage:
  • Without considering similarity among different words
  • it has the same drawbacks as one-hot vector
    

1.4 n-gram model

N-gram model is an extension of bag of word model. While bag-of-word model considers each word only, N-gram model considers a tuple of n consecutive words as an element in the collection of words.

Example: Consider a sentence: “a boy is playing grames”.

When using 3-gram model, the collection of words becomes

{(a boy is), (boy is playing),(is playing games)}

Then if we have a 3-gramm vector for a document: [1, 0,0 ], it means the element (a boy is) appear once in the document.

• Advantage:
  • More flexible and robust than bag-of-world model, since it could considers different structure of words. Some names like “deep learning”, “machine learning” with more than one words can be detected easier.
• Disadvantage:
  • The collection could be large when using different grams. Usually, bigram and trigram are used.
    

1.5 Word Vectors/ Word Embeddings/Word distributed representations

Word Vectors represent words by context. Context of a word is a set of words that appear nearby, or in a fixed window A word meaning is given by the words that frequently appear close-by.

Each entry in a word vector for a word is the similarity between this center word and the words in context.

Eg: In “I like dog”, vector for “like” = [0.01,0.7 ,0.5], where 0.5 is the possibility “dog” will occur, given center word “like”.

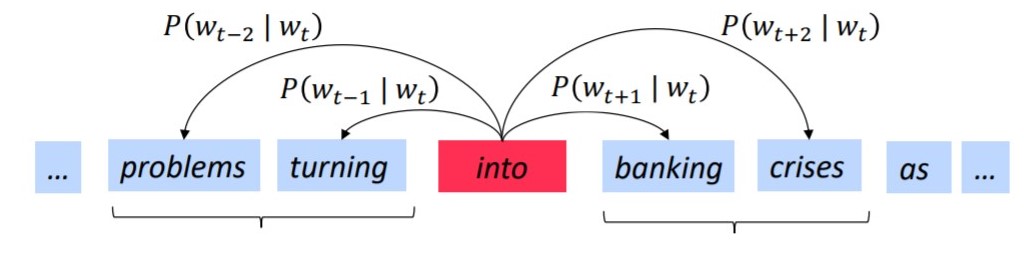
More general, given the center word $w_{t}$, the possibility of context word $w_{t+1}$ will occur is $P(w_{t+1}|w_{t} )$. Then in word vector, our goal is to find the best condition distribution to represent the vector. There are many frameworks to find word vector, such as word2Vec, Glove, Fasttext.

• Advantage:
  • Able to compute similarity between words
  • No need to label by human
• Disadvantage:
  • Dimension of vector is equal to the number of words in vocabulary. It could be very large
  • Need to learn the similarity by word2vector framework. Hard to compute similarity when there is a large corpus of words

2. Word2Vector: Skip-gram

A framework to learn and find dense word vectors, rather than sparse orthogonal vector like bag-of-word model. Here is details about word2vector

The dense word vectors measure similarity between two words. If two words are similar, then they have similar word vectors.

Goal: to learn the word vector that measure the similarity between context and center word, Or possibility that the next word will occur, given the center word.

2.1 Summary of Idea in Word2Vector:

1. Collect a large corpus of text
2. Represent each word in text as a vector (count vector or one-hot model)
3. Go through each position t in text, find center word c and outside words o (context words)
4. Find similarity of the word vectors for c and o (c and o are actually from the output of the neural network), compute possibility of context o, given center word vector c
5. Keep adjusting word vectors / train the network to maximize possibility/likelihood function and find the optimal word vectors that contains similarity between c and o.
6. Note: input to network is one-hot vector , output to network is similarity/possibility vector. The output is the vector we want

2.2 One-hot Vector

• In Skip gram, it first find the set of vocabularies and then converts each word into its one-hot vector. In one-hot vector, 1 represents the word

• Example:
  consider a sentence “I like dog and you like cat”.
  Then there is a set of words [“I”,”you” ,”like””,”dog”,”cat”,”and”].

  word	one-hot vector
  “I”	[1,0,0,0,0,0]
  “like”	[0,1,0,0,0,0]
  “dog”	[0,0,1,0,0,0]
  “and”	[0,0,0,1,0,0]
  …	…

  Then one-hot vector for “like” = [0,0,1,0,0,0], where 1 at the corresponding position represents “like” in the word set.
  Dimension of vector = |V| , where V is vocabulary set of the text.

2.3 Skip-gram neural network

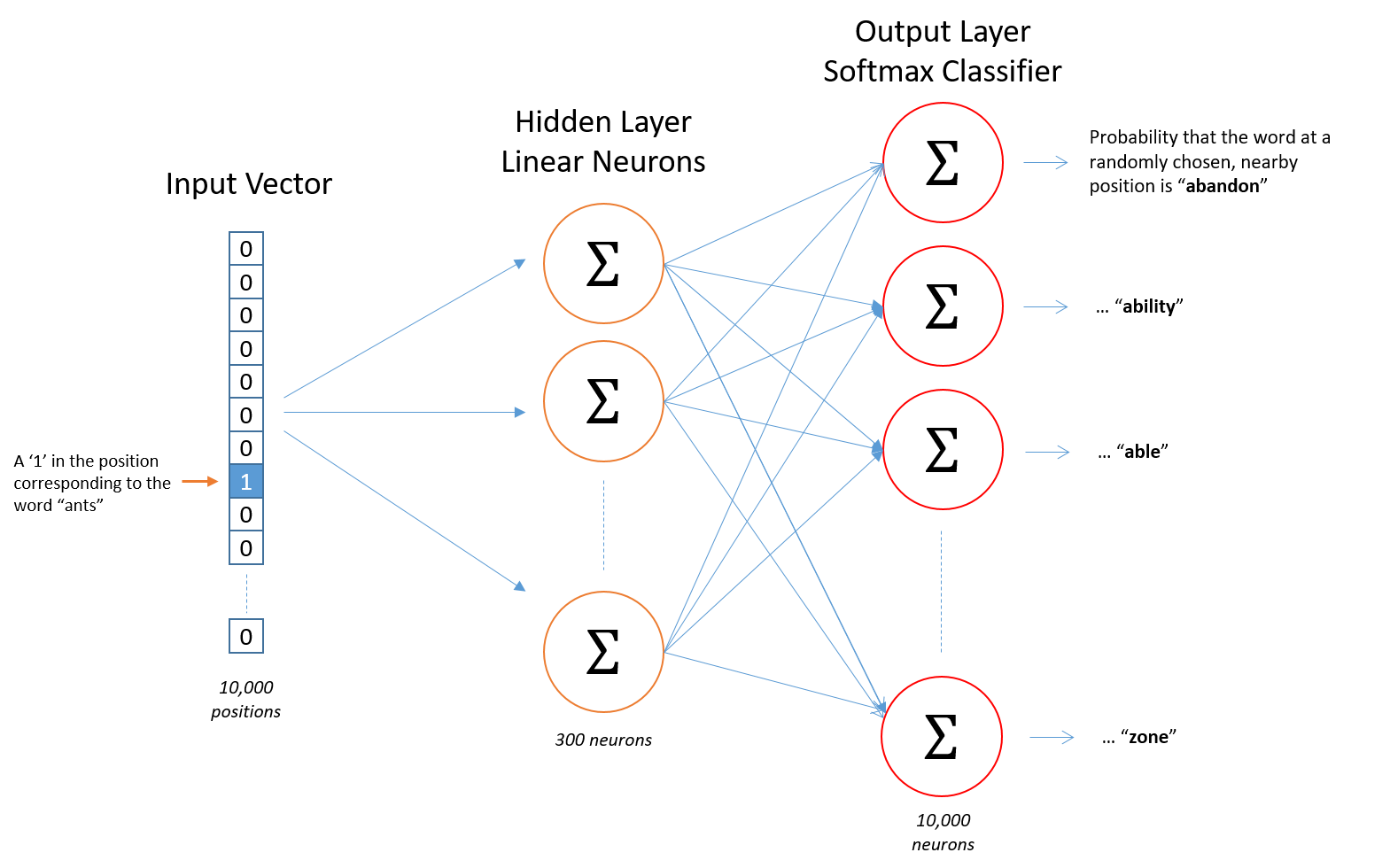
• The neural network takes one-hot vector as input, with size |V|. Let denote one-hot vector as v for convenience

• There are only one hidden layer. There is no activation function in this layer and hence it is linear. The number of neurons N is defined by user.

• Softmax activation function for output with |V| neurons

• There is a input weight matrix W with dimension |V|-by-N between input layer and hidden layer (|V| rows and N columns)

• There is a input weight matrix W ‘ with dimension N-by-|V| between hidden layer and output layer

• Since input is 0,1 vector, when it times input matrix W, it actually selects a row of the matrix.
  Hence, we can consider W as a look-up table and output from hidden layer c = Wv is the real “word vector”.

• “Word vector” is acutually one-hot vector or bag-of-word vector times input weight matrix W

• The i^th entry in the output vector from softmax function is the possibility that if you pick up a word nearby the input word, that is the i^th word in the vocabulary.

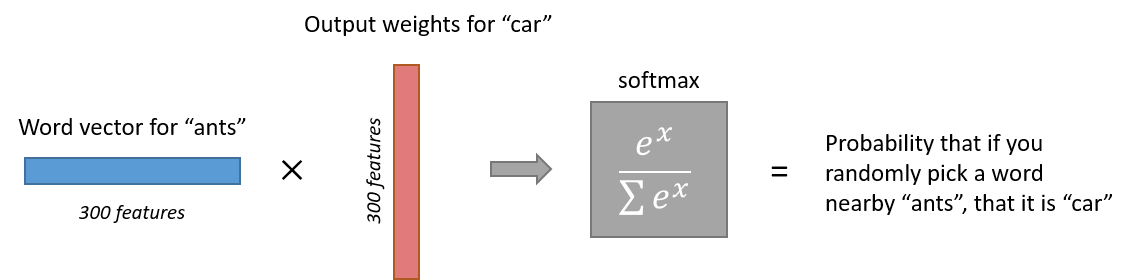
Note:

1. when training neural network, its output is one-hot vector ( set the maximum softmax output value as 1, others as 0s), indicating the predicted nearby context words
2. When evaluating network, using softmax output value, possibility as output, to compute the cost value
3. __Since there are different actual context words $w_{t-1}, w_{t-2}, …$, corresponding to the single input vector $w_{t}$.__
   If we consider P($w_{t-1},w_{t-2},w_{t-3}|w_t$) with window with size of 4 containing central word $w_t$ and context words $w_{t-1},w_{t-2},w_{t-3}$,
   then the output look something like this: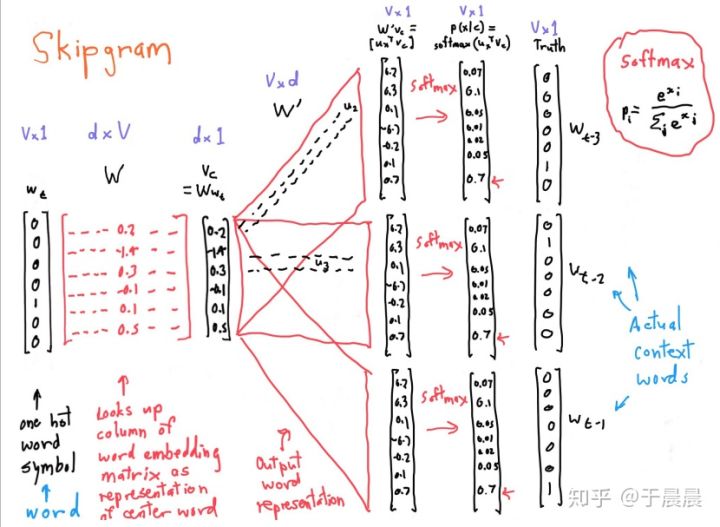

2.4 Evaluation of Skip-gram

Since the input to the network is a single word, it is also regarded as center word $w_t$, at the t position in text. The words nearby it are called context, or outside words. The context word at t+k position, is denoted as $w_{t+k}$.

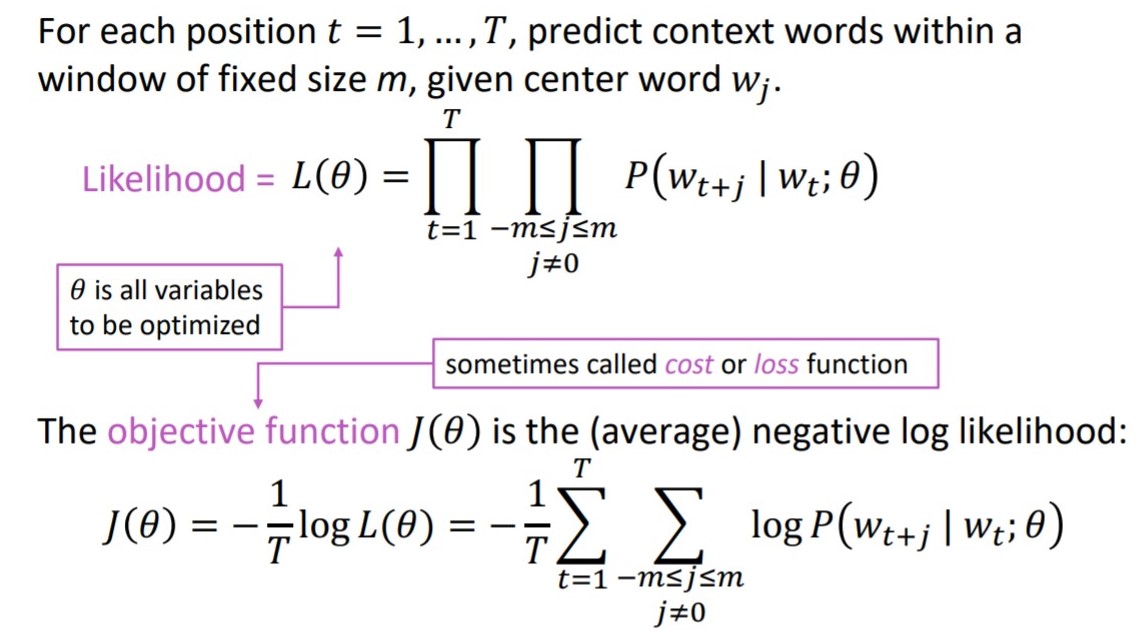
Hence our goal, or objective is to estimate the distribution $P(w_{t+k}| w_{t})$.
The distribution has the meaning that given center word $w_t$, the possibility that context word $w_{t+k}$ will appears.

In order to estimate the distribution, we need to maximize the likelihood function, or its log value, called loss, or cost function, shown as below.

Advantages

• It is unsupervised learning hence can work on any raw text given.
• It requires less memory comparing with other words to vector representations.
• It requires two weight matrix of dimension [N, |v|] each instead of [|v|, |v|]. And usually, N is around 300 while |v| is in millions. So, we can see the advantage of using this algorithm.

Disadvantages

• Finding the best value for N and the context position is difficult.
• Softmax function is computationally expensive.
• The time complexity for training is high

Models for Word2vector

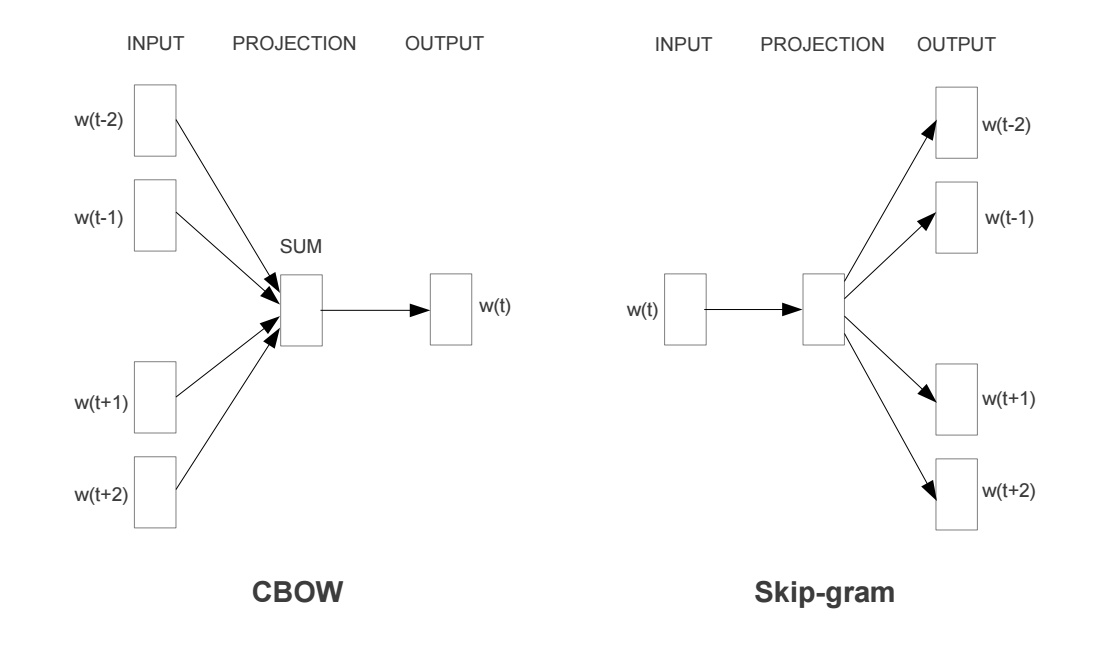
1. Skip-gram
   Predict context (outside) words (surrounding the center word) given center
   word
2. Continuous Bag of words （CBOW）
   Predict center word from (bag of) context words. It is an inverse version of skip-gram.

Reference:

[1] http://mccormickml.com/2016/04/19/word2vec-tutorial-the-skip-gram-model/
[2] http://web.stanford.edu/class/cs224n/slides/cs224n-2020-lecture02-wordvecs2.pdf
[3] https://towardsdatascience.com/skip-gram-nlp-context-words-prediction-algorithm-5bbf34f84e0c
[4] https://zhuanlan.zhihu.com/p/50243702
[5] http://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf