NLP Improvement on Word2Vector
Introduction
Although word2Vec for word embedding has been widely used, it has some obvious shortages that affect computation of word vector. This passage is to identify those shortages and introduce a solution called Negative Sampling to solve the problems.
Review to Word2Vec
Word2Vec is a framework to convert vocabulary in texts into dense numeric vector representation such that our machine learning models can realize the vocabulary and human language and learn something.
The main idea of word2Vec (skip-gram) is following:
Start with random word vectors in neural network
Iterate each world in word corpus
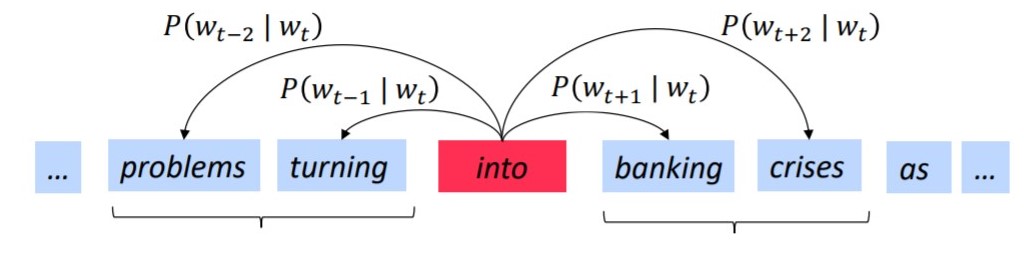
Predict the context words (surrounding words) of a center word by computing posterior distribution: $P(w_{t+1}|w_t)$, where $w_t$ is the center word at position t and $w_{t+1}$ is the surrounding word.
$$P(o|c) = \frac{exp(\textbf{u}_o^T\textbf{v}c )}{\sum{w\in V} exp(\textbf{u}_w^T\textbf{v}_c)}$$
where $\textbf{v}_c$ is the word vector of center word and $\textbf{u}_o$ is the word vector of surrounding words (or weights).
- Update word vector using Gradient Descent based on cost function
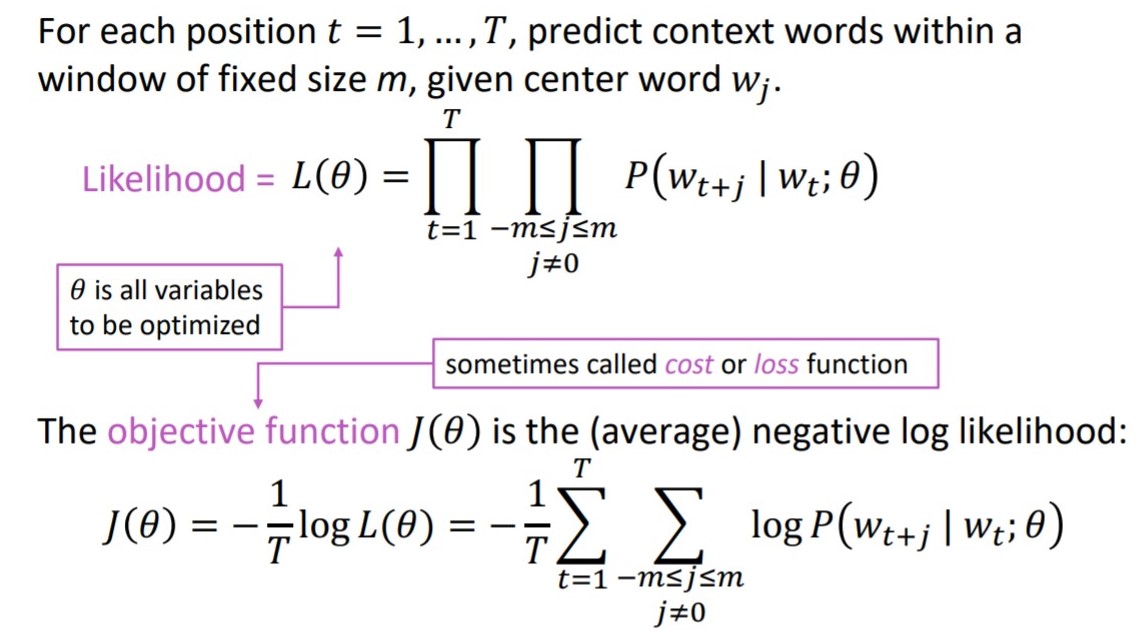Note: $\theta$ in loss function here is the weight matrix used in softmax. The weight matrix in the network is $\textbf{u}_w$.
Disadvantages of Word2Vector
We can notice that bigger vocabulary it is, larger the word vector becomes. Usually, there are thousands of different words in text, using gradient descent to update the whole weight matrix leads to expensive computation cost and each update become super slow. We need to repeat updating each weight using the following equation and the time complexity increases linearly as the amount of words increases.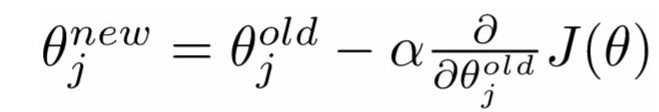
Improvement
Stochastic Gradient Descent with sampled window
Assume we are using a window centered at center word and hence it has size of 2m+1. The the update is
- Repeatedly sample windows and iterate each window, rather than iterate all windows.
- Compute the gradient of the words that actually appear. The graident of words in dictionary that don’t appear in text won’t be updated.
Notes:
the gradient of the words that don’t appear in text, but in vector is all 0. In this case the vector would be very sparse (many zeros in vectors). It is a waste of time to compute those 0 update.
We need a sampling technique to sample windows and words for updating part of weights. This leads to our next section Negative Sampling
Negtive Sampling
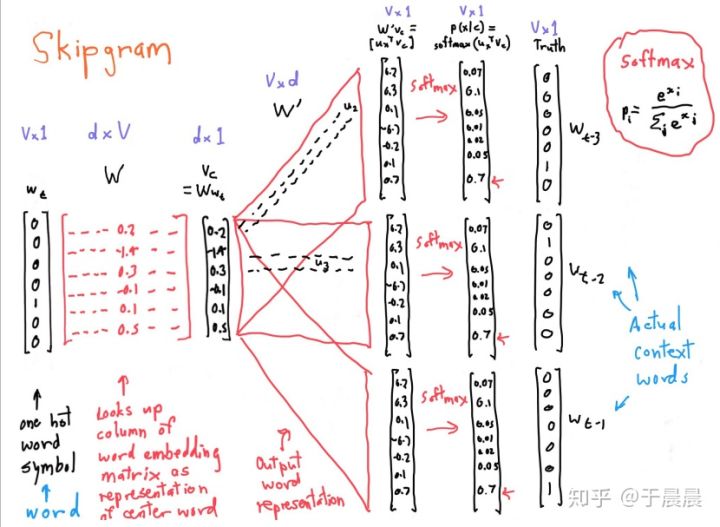
In word2vec (skip-gram), the input to the neural network is one-hot word vector of the center word. In training step, output of neural network is a vector of possibility that each word can appear given the center word.
In prediction step, the output is converted from possibility vector to one-hot vectors of the predcited context words that are most likely to appear given the center word. For example, if we have possibility output [0.1, 0.1, 0.5, 0.3] and expect predictions of 2 context words. Then we output one-hot vectors of the words with possibility of 0.5 and 0.3.
The targets corresponding to the given center word are one-hot vector of context words surrounding this center word in the window.
Negative words
In one-hot vector output from neural network, we call the word with value equal to 1 as postive word and those words with values equal to 0 as negative word.
For example. Assume we have a word vector with dimension of 100 (100 words in dictionary). Then in a window such as “I like my dog”,
| I | like | my | dog |
|---|
if “like” is center word $w_t$, as the input to the neural network. Then “I” , “my”, “dog” are context words, or positive words that are expected to output “1” in the output one-hot vector of neural network(it is expected to output 3 one-hot vectors). Then other words that don’t appear in this window / context and are expected to be 0 in one-hot vector are negative words.
Selection of negative words
However, there would be a large amount of negative words that don’t appear in context. If we update weights of all negative words, the update could be very inefficient.
In negative sampling, we sample negative words based on the possiblity that word may occur. The possibility is given by:
$$
P(w_i)= \frac{f(w_i)}{\sum_j^Nf(w_j)}$$
where $f(w_i)$ is the number of word $w_i$ appears in corpus and the denominator is the number of all words appear/ the amount of words in corpus.
However, the author proposes this equation since it gives the best performance.
$$
P(w_i)= \frac{f(w_i)^{3/4}}{\sum_j^Nf(w_j)^{3/4}}$$
Based on the possibility of the occurence of words, we can sample a number of negative words that are most likely to appear and update the corresponding weights by backward update in neural network. The number of samples is set by user.
For example, If we have a dictionary with size of 100 words (hence one-hot vector with size of 100) and each word has corresponding weights with size of 100. Then there are 100x100 weights to update when updating all weights in network. However, if we only sample 20 negative words to update, we need to update 20x100 weights only. This allows us to speed up training step.
References
[1] http://mccormickml.com/2017/01/11/word2vec-tutorial-part-2-negative-sampling/