Data Structure9 minutes read (About 1297 words)  0 visits

Data Structure 3 - BinaryTree

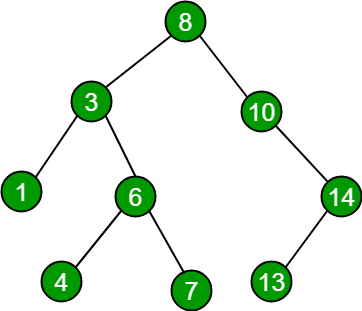
Binary Tree

Definition of Binary Tree

The settings of binary tree are following:

  1. Each node in the tree contains no more than 2 children nodes (left node, right node)
  2. Leaf nodes of the tree are the nodes that contain no children nodes

Traversal of Binary Tree

Type of traversals of binary tree

Consider this example of binary tree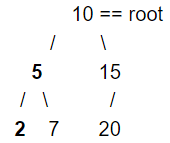

  1. Pre-order traversal
    The order of visiting nodes: current node -> left children node -> right children node.
    In the binary tree above, we start from the root node (current node) and follow the rule to visit each node. Then have cur_node= 10, left_node =5. when we goes to left_node 5, 5 becomes the new current node and hence print 5 and then its left_node 2. When it finds there is no left node after 2, it goes back to 5 and visit its right node.
    Repeat doing this, we have Pre-Order traversal of this binary tree: 10-> 5->2-> 7-> 15->20

  2. In-order traversal
    The order of visiting nodes: left children node -> current node -> right children node
    Similar to Pre-Order traversal, except the traversal order, In-order requires the current node is the second node to be visited. Hence, In-Order traversal of this example is: 2->5->7->10->15->20

  1. Post-order traversal
    The order of visiting nodes: left children node -> right children node -> current node
    Similarly, Post-Order traversal of the example is: 2->7->5->15->20->10
  1. Level-order traversal
    It traverses the binary tree from top level to lower level. In each level of tree, it iterates the nodes from left to right. Level-Order traversal of this example: 10->5->15->2->7->20

Implementation of Traversal of Binary Tree

  1. Recursive Method

  • Pre-Order
    Time Complexity: O(n)
    Memory Complexity: O(h), h is the height of the tree. It is used by recursion to store address of function in stack

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    class TreeNode():
        def __init__(self):
            self.left = None
            self.right = None
            self.val = None
    class Solution():
        def Pre_Order(self, root):
            if not root:
                return []
            result = []
            result.append(root.val)
            left_list = self.Pre_Order(root.left)
            right_list = self.Pre_Order(root.right)
            result.extend(left_list)
            result.extend(right_list)
            return result

  • In-Order
    Time Complexity: O(n)
    Memory Complexity: O(h), h is the height of the tree. It is used by recursion to store address of function in stack

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    class Solution():
        def In_Order(self, root):
            if not root:
                return []
            result = []
            left_list = self.In_Order(root.left)
            result.extend(left_list)
            result.append(root.val)
            right_list = self.In_Order(root.right)
            result.extend(right_list)
            return result

  • Post-Order
    Time Complexity: O(n)
    Memory Complexity: O(h), h is the height of the tree. It is used by recursion to store address of function in stack

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    class Solution():
        def Post_Order(self, root):
            if not root:
                return []
            result = []
            left_list = self.Post_Order(root.left)
            result.extend(left_list)
            right_list = self.Post_Order(root.right)
            result.extend(right_list)
            result.append(root.val)
            return result
  1. Iterative Method
  • Pre-Order
    Time Complexity: O(n)
    Memory Complexity: O(h), h is the height of the tree
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    class Solution(object):
      def PreOrder(self, root):
        """
        input: TreeNode root
        return: Integer[]
        """
        # write your solution here
        if not root:
          return []
        stack = [(root, 1)]
        result = []
        while len(stack)>0:
          node, count = stack.pop()
          if count ==1:
            result.append(node.val)
            stack.append((node,2))
            if node.left:
              node = node.left
              stack.append((node, 1))
          if count == 2:
            if node.right:
              node= node.right
              stack.append((node,1))
        return result
  • In-Order
    Time Complexity: O(n)
    Memory Complexity: O(h), h is the height of the tree
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    class Solution(object):
      def InOrder(self, root):
        """
        input: TreeNode root
        return: Integer[]
        """
        # write your solution here
        if not root:
          return []
        stack = [(root, 1)]
        result = []
        while len(stack)>0:
          node, count = stack.pop()
          if count ==1:
            stack.append((node,2))
            if node.left:
              node = node.left
              stack.append((node, 1))
          if count == 2:
            result.append(node.val)
            if node.right:
              node= node.right
              stack.append((node,1))
        return result
  • Post-Order
    Time Complexity: O(n)
    Memory Complexity: O(h)
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    class Solution(object):
      def PostOrder(self, root):
        """
        input: TreeNode root
        return: Integer[]
        """
        # write your solution here
        if not root:
          return []
        stack = [(root, 1)]
        result = []
        while len(stack)>0:
          node, count = stack.pop()
          if count ==1:
            stack.append((node,2))
            if node.left:
              node = node.left
              stack.append((node, 1))
          if count == 2:
            stack.append((node, 3))
            if node.right:
              node= node.right
              stack.append((node,1))
          if count==3:
            result.append(node.val)
        return result
  • Level-Order
    Time Complexity: O(n)
    Memory Complexity: O(h)
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    class Solution(object):
        def LevelOrder(self,root):
            if not root:
                return []
            queue = [root]
            result = []
            while len(queue) >0:
                # dequeue
                node = queue[0]
                del queue[0]
                result.append(node.val)
                # enqueue
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            return result

Special Binary Tree

1. Balanced Binary Tree

Balanced Binary Tree is a tree that the depth of left and right subtrees of every node differ by 1 or less.
Hence, for each node in the tree, we need to check the heights of left, right subtrees.
In the examples below:

Example 1 is a balanced tree, but Example 2 is not, since left and right subtrees of the node of 20 in example 2 has the height difference 2-0 = 2 >1.

2. Complete Binary Tree

A Binary Tree is a complete Binary Tree if all the levels are completely filled except possibly the last level and the last level has all keys as left as possible
Consider the following example:

1
2
3
4
5
     10
    /   \ 
   5     1
 /  \   /  
2    4  2

This is an complete as well as balanced tree.
However, the following one is balanced but not complete tree, since in the last level, all keys are not as left as possible as the node 2 should be in the left node, but it doesn’t.

1
2
3
4
5
     10
    /   \ 
   5     1
 /  \     \
2    4      2

4. Perfect Binary Tree

Perfect Binary Tree A Binary tree is a Perfect Binary Tree in which all the internal nodes have two children and all leaf nodes are at the same level.

Example of a perfect tree

1
2
3
4
5
     10
    /   \ 
   5     1
 /  \    / \
2    4  3    2

Example of not a perfect tree

1
2
3
4
5
     10
    /   \ 
   5     1
 /  \    /
2    4  3

This is a complete, balanced binary tree, but not a perfect tree

5. Binary Search Tree

Binary search tree is a tree that for every node in the tree, the values in left subtree are smaller than its value, the values in right subtree are greater than its.
if we consider the duplicated values in the tree, the values in right subtree can be greater than or equal to the node value. This case should be discussed if duplicated values exist. This difference should be determined when discussing with the hiring manager

Example of Binary Search Tree

1
2
3
4
5
     10
    /   \ 
   5     11
 /  \     \
2    7     21

Example of Not a Binary Search Tree

1
2
3
4
5
     10
    /   \ 
   5     1
 /  \     \
2    7     21

6. AVL Tree

AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes.
When inserting each element in the AVL tree, it will re-balance the tree automatically.
The operations of this data structure will be demonstrated in future

7. Red-Black Tree

Red-Black tree is also a self-balancing tree. It has the following constraints:

  1. Each node has a color either red or black
  2. Root of tree is always black
  3. No adjacent red nodes. The parent/ children of a red node could not be red. But there could be adjacent black nodes
  4. Every path from a node (including root) to any of its descendant NULL node has the same number of black nodes.
    Example:

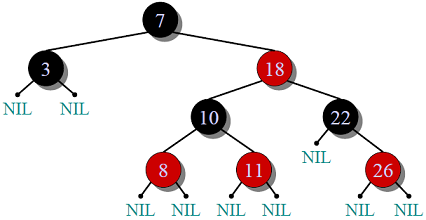
Every path starting from node 18 to NiL/ None, have the same amount of black node 1.

Summary

In future, I may write the notes about more operations about binary tree, AVL tree, Red-Black Tree, just like computing height of tree, isBalanced, isSymmetric, insertion and deletion of element in AVL tree/Red-Black tree

Reference

[1] https://www.geeksforgeeks.org/red-black-tree-set-1-introduction-2/
[2] https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
[3] https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%85%83%E6%90%9C%E5%B0%8B%E6%A8%B9

#

Comments

Links

Categories

Tags

Amdahl's Law1
Backpropagation1
Bagging1
BeautifulSoup1
Binary Tree1
Blending1
Boosting1
Boosting Machine1
BuckSort1
C++1
Collaborative Filtering1
Confusion Metric1
Convolution Neural Network1
Cross Validation1
D3.js1
DCN1
DIN1
Data Analysis1
Data Mining2
Data Visualization1
Datawhale Team Learning2
DeepFM1
Dropout1
EGES1
Ensemble Learning6
FFM Model1
GATE1
GNN8
Graph8
Graph Embedding1
Holdout1
Hypothesis Test1
Independence Test1
Installation1
JavaScript1
K-Mean Clustering1
KMean Clustering1
LGBM2
Machine Learning1
Markdown1
Model Evaluation1
Model Selection1
Natural Language Representations1
Nature Language Processing1
Negative Sampling1
NeuralFM1
P-value1
Parallel Computing1
Parallel Speedup1
PySpark1
ROC curve1
Recommendation System1
Regression1
Regular Expression1
Scala1
Shell Tutorial1
Sorting1
Spark1
Stacking2
Swing1
Traversal1
Tutorial1
Unsupervised Learning1
Variable Selection1
WSDM1
Web Scrapping1
Wide and Deep1
Wide and Deep Model1
Wide&Deep Model1
Word Embedding1
Word vector1
binary search1
bubble sort1
commands1
insertion sort1
merge sort1
non-parametric learning1
quick sort1
review1
statistic analytics tool1

Recent

Archives

Subscribe to Updates

Follow
×