2021-07-09Deep Learning21 minutes read (About 3108 words) 0 visits

GNN-8-Conclusion

GNN-Task-8-Conclusion

1. Introduction

这一节我们来总结一些之前学过的GNN的常见任务，GNN模型, 以及torch_geometric的常用类型，比如Dataset， ClusterData, Mini-batching等。另外也总结一下不同的GNN模型的常用场景和特点等。

2. GNN Tasks

Definition of Graph
- 一个图被记为 $\mathcal{G}={\mathcal{V}, \mathcal{E}}$，其中 $\mathcal{V}={v_{1}, \ldots, v_{N}}$ 是数量为 $N=|\mathcal{V}|$ 的结点的集合， $\mathcal{E}={e_{1}, \ldots, e_{M}}$ 是数量为 $M$ 的边的集合。
- 图用节点表示实体（entities ），用边表示实体间的关系（relations）。
- 节点和边的信息可以是类别型的（categorical），类别型数据的取值只能是哪一类别。一般称类别型的信息为标签（label）。
- 节点和边的信息可以是数值型的（numeric），类别型数据的取值范围为实数。一般称类别型的信息为属性（attribute）。
- 大部分情况中，节点含有信息，边可能含有信息。
Types of Graph
- 同质图（Homogeneous Graph）：只有一种类型的节点和一种类型的边的图。
- 异质图（Heterogeneous Graph）：存在多种类型的节点和多种类型的边的图。
- 二部图（Bipartite Graphs）：节点分为两类，只有不同类的节点之间存在边。
Node Embedding
在Graph里面, node representation和edge的表示是分别用两个矩阵表示，其中node representation/embedding 的shape = [Num_nodes, dimension of node embedding], 而 edge的matrix的shape = [2, number of edge], 其中 edge_index[0] = source nodes, edge_index[1]= target nodes
Node Prediction(Classification , Regression)
预测节点的类别或某类属性的取值, 例子：对是否是潜在客户分类(Node Classification) ,对游戏玩家的可以消费的金额做预测(Node Regression)
Link Prediction
预测两个节点间是否存在链接, 例子：Knowledge graph completion、好友推荐、商品推荐(有点类似Matrix Factorization里面的对item和user相似度关联度预测)
Graph Embedding
Graph embedding/representation 是可以通过node embedding通过pooling或者concatenate 拼接得到的
Graph Prediction
对不同的图进行分类或预测图的属性, 例子：分子属性预测, 对分子结构组成(分子的组成结构就是一个图)进行分类
Other Tasks
1. Graph Generation：例如药物发现
2. Graph Evolution：例如物理模拟图演变

3. PyG Toolkits

Dataset

InMemoryDataset
- Link: GNN-Task-4-LinkPrediction
- torch_geometirc source code: https://pytorch-geometric.readthedocs.io/en/latest/_modules/torch_geometric/data/in_memory_dataset.html#InMemoryDataset
InMemoryDataset是一个用于把raw数据全部转换成torch的 .pt 数据之后，把所有数据加载到内存里面的的数据集。由于它把数据集全部加载到内存里面，所有它的数据读取速度快，但是不能存放超大型的图数据。因此它一般用于中小型图数据
ClusterDataset
- Link: GNN-Task-5-ClusterData
- torch_geometirc source code: https://pytorch-geometric.readthedocs.io/en/latest/_modules/torch_geometric/data/cluster.html#ClusterData
ClusterDataset是根据ClusterGCN的paper针对超大型图数据计算时neighborhood expansion problem 导致梯度计算复杂度指数增长的问题进行优化。它把整个图通过clustering partition的方法得到独立的subgraph然后再梯度更新。
Mini-Batching Dataset
- Link: GNN-Task-6-GIN-GraphEmbedding , GNN-Task-7-Mini-Batching
- torch_geometirc source code: https://pytorch-geometric.readthedocs.io/en/latest/_modules/torch_geometric/data/data.html#Data
根据官方文档, Mini-Batching 简单地通过把一个大型图的Adjacency matrix 按照对角线方向拆分成多个小batch，每个batch代表一个独立的subgraph. 然后它把这些subgraph作为一个batch去feed GNN。Note：虽然整个adjacency matrix被划分成多个batch，但是GNN的输入的shape (node的个数等)不用变，因为Adjacency Matrix里面每个subgraph相互独立没有相互连接，所以训练时不会涉及不同的graph的node的计算。(这样就有些想把整个图通过一个mask把一些node和edge隐藏起来进行计算)

和前面的ClusterDataset对比，Mini-Batching 有以下不同:
- Mini-Batching(像 PCQM4M分子数据集)它是基于InMemoryDataset,用起来和普通图数据一样，它可以通过 split_idx函数获取train, test, valid的mask对图进行拆分，并且可以像普通数据集一样直接用DataLoader 进行分batch训练
- 而它也不像ClusterDataset那样要想通过cluster进行subgraph clustering和采样，所以数据加载更快
- Mini-Batching的dataset是储存在Sparse Matrix里面只对非零的数据进行储存，所以没有大量的存储开销

4. GNN Models

4.1 MessagePassing

在图神经网络里面，在对数据和样本之间的关系进行建模得到图的edge， node之后，我们需要在图里面把每个节点的信息根据它的neighbor的信息进行更新，从而达到node的信息更新和节点特征(Node Representation)的特征表达。而这个把node节点信息相互传递从而更新节点表征的方法也叫Message Passing。
MessagePassing是一种聚合邻接节点信息来更新中心节点信息的范式(通用架构)**，它将卷积算子推广到了不规则数据领域，实现了图与神经网络的连接。遵循消息传递范式的图神经网络被称为消息传递图神经网络。
**Message Passing GNN的通用公式可以描述为
$$
\mathbf{x}_ i^{(k)} = \gamma^{(k)} ( \mathbf{x}_ i^{(k-1)}, \square_{j \in \mathcal{N}(i)} , \phi^{(k)}(\mathbf{x}_ i^{(k-1)}, \mathbf{x}_ j^{(k-1)},\mathbf{e}_{j,i}) ),
$$

根据官方文档以及CREATING MESSAGE PASSING NETWORKS, 我们定义
+ $\mathbf{x}^{(k-1)}_i\in\mathbb{R}^F$表示神经网络的$(k-1)$层中节点$i$的节点表征

+ $\mathbf{e}_{j,i} \in \mathbb{R}^D$ 表示从节点$j$到节点$i$的边的属性信息。

+ $\square$表示**可微分**的、具有排列不变性（**函数输出结果与输入参数的排列无关**）的函数, 比如aggregation 函数。比如sum， mean, min等函数和输入的参数顺序无关的函数。

+ $\gamma$ : **可微分可导**的update 函数，比如MLPs（多层感知器）

+ $\phi$: **可微分可导**的message 函数，比如MLPs（多层感知器）和 linear Projection等

4.2 GCN

GCN 原理
根据PyG的官方文档，**GCNConv** 的公式是
$$
\mathbf{x}_ i^{(k)} = \sum_{j \in \mathcal{N}(i) \cup { i }} \frac{1}{\sqrt{\deg(i)} \cdot \sqrt{\deg(j)}} \cdot ( \mathbf{\Theta} \cdot \mathbf{x}_ j^{(k-1)} ),
$$

矩阵的形式是
$$
\mathbf{X}^{(k)} = \mathbf{D}^{-0.5}\mathbf{A}\mathbf{D}^{-0.5}\mathbf{X}^{(k-1)}\mathbf{\Theta}
$$

其中，$\mathbf{x}_i$ 的节点的特征是由它的近邻的node的信息(包括node i自己)进行更新，所以计算时j是节点i的邻居(包括节点i本身)的子集里面的node。邻接节点的表征$\mathbf{x}_j^{(k-1)}$首先通过与权重矩阵$\mathbf{\Theta}$相乘进行变换，然后按端点的度$\deg(i), \deg(j)$进行归一化处理，最后进行求和。这个公式可以分为以下几个步骤：
1. 向邻接矩阵添加自环边。
2. 对节点表征做线性转换。
3. 计算归一化系数。
4. 归一化邻接节点的节点表征。
5. 将相邻节点表征相加（”求和 “聚合）。
GCN存在的问题: Oversmoothing
根据paper Tackling Over-Smoothing for General Graph Convolutional Networks, over-smoothing issue drives the output of GCN towards a space that contains limited distinguished information among nodes, leading to poor expressivity. 即随着GCN层数加深, GCN的node embedding的信息就会越来越相似缺少差异性(就相当于丢失信息了)，导致特征的表达能力不足。不过这个现象也是很正常的，回想一下CNN, 如果Convolution layer 过多，就会导致对输入特征作用的范围越来越大，把一大块的特征过滤成一小块输出，表达的信息就会丢失更多。另外，也可以把Convolution看成是一个低通滤波器，如果这个filter作用范围越大，输出的信号越平滑，那么就会丢失很多信息了。

4.3 GAT

paper link: https://arxiv.org/pdf/1710.10903.pdf
Graph Attention Network 的attention公式如下:

$$
\alpha_ {i,j} = \frac{ \exp(\mathrm{LeakyReLU}(\mathbf{a}^{\top}
[\mathbf{W}\mathbf{h}_ i , \Vert , \mathbf{W}\mathbf{h}_ j]
))}{\sum_ {k \in \mathcal{N}(i) \cup { i }}
\exp(\mathrm{LeakyReLU}(\mathbf{a}^{\top}
[\mathbf{W} \mathbf{h}_ i , \Vert , \mathbf{W}\mathbf{h}_ k]
))}.
$$

节点信息更新
$$
\mathbf{h}_ i^{‘} = \sigma(\frac{1}{K} \sum_ {k=1}^K\sum_ {j \in N(i)} a_{ij}^{k}\mathbf{W}^k\mathbf{h}_ {i})
$$

实际上GAT就是在每个节点把邻居的信息聚合时根据邻居节点的node representation和这个节点的node representation的相似度对聚合的信息有侧重地聚合
其中每个参数的代表:

$\mathbf{h}_i$: 节点 i的node representation。这个node representation可以是GNN的某一层的输出
$\mathbf{W}$: shared linear transformation. 用于每个节点的共享的线性投映矩阵，所有节点都用相同的W进行投映
$k \in \mathcal{N}(i) \cup { i }$: 第i个节点的邻居节点(包括第i个节点本身)。注意因为这里涉及两个sum，两个loop所以计算有点慢
$\Vert$: 把两个向量拼接

4.4 GraphSAGE (Graph Sample and Aggreate Graph Embedding)

GraphSAGE是一种 inductive的representation learning的方法，就是归纳法。它是用于预测之前没有见过的node的embed的ing的特征。它的主要思想是通过学习多个aggregate函数(paper里面提出来mean, LSTM, pooling 三个)，然后这些aggregate函数用neighbor的信息来生成之前没有见过的node的embedding之后再做预测。下面是GraphSAGE的流程图：

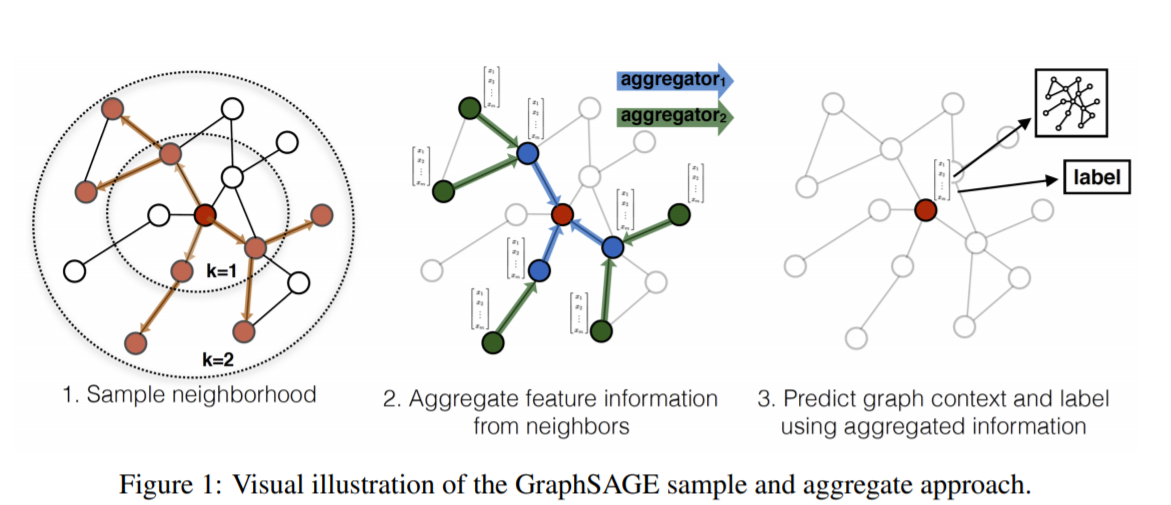
GraphSAGE 的node embedding的其中一个生成公式为(还有其他用于生成embedding的aggregate函数公式可以参考原文):
$$
\mathbf{x}_ {i}^{‘} = \mathbf{W}_ {1}x_{i} + \textbf{mean}_ {j \in N(i)}(\mathbf{x}_{j})
$$
GraphSAGE 的graph-based unsupervised loss function 定义为

$$
\mathbf{J}_ {G}(z_{u}) = -log(\sigma(\mathbf{z}_ {u}^{T}\mathbf{z}_ {v})) - \mathbf{Q} \cdot \mathbf{E}_ {v_ {n} \in P_ {n}(v)}log(\sigma(-\mathbf{z}_ {u}^{T} \mathbf{z}_ {v_{n}}))
$$

其中:

$j \in N(i)$ 为第i个节点的第j个neighbor节点
$v$ 是和 $u$ 在定长的random walk采样路径出现的节点
$Q$ 是负样本的个数， $P_{n}(v)$ 是负采样的分布
$z_{u}$是node representation特征
这里$\sigma()$里面计算的是节点和random walk采样时同时出现的其他节点的相似度。相似度越大，loss越小

4.5 GIN

GIN 全称是Graph Isomorphsim Network, 同构图网络，是用于学习Graph Embedding的一种网络，它也可以用来测量两个图之间的相似度。

在GIN里面node representation的update公式是
$$
h_ {v}^{k} = \text{MLP}^{k}((1+ \epsilon^{k})h_ {v}^{(k-1)} + \sum_ {u \in \mathbf{N}(v)} h_ {u}^{(k-1)})
$$

在生成节点的表征后仍需要执行图池化（或称为图读出）操作得到图表征，最简单的图读出操作是做求和。由于每一层的节点表征都可能是重要的，因此在图同构网络中，不同层的节点表征在求和后被拼接，其数学定义如下，
$$
h_ {G} = \text{CONCAT}(\text{READOUT}({h_{v}^{(k)}|v\in G})|k=0,1,\cdots, K)
$$
采用拼接而不是相加的原因在于不同层节点的表征属于不同的特征空间。未做严格的证明，这样得到的图的表示与WL Subtree Kernel得到的图的表征是等价的。